There are two ways to teach quantum mechanics. The first way -- which for most physicists today is still the only way -- follows the historical order in which the ideas were discovered. So, you start with classical mechanics and electrodynamics, solving lots of grueling differential equations at every step. Then you learn about the "blackbody paradox" and various strange experimental results, and the great crisis these things posed for physics. Next you learn a complicated patchwork of ideas that physicists invented between 1900 and 1926 to try to make the crisis go away. Then, if you're lucky, after years of study you finally get around to the central conceptual point: that nature is described not by probabilities (which are always nonnegative), but by numbers called amplitudes that can be positive, negative, or even complex.
Today, in the quantum information age, the fact that all the physicists had to learn quantum this way seems increasingly humorous. For example, I've had experts in quantum field theory -- people who've spent years calculating path integrals of mind-boggling complexity -- ask me to explain the Bell inequality to them. That's like Andrew Wiles asking me to explain the Pythagorean Theorem.
As a direct result of this "QWERTY" approach to explaining quantum mechanics - which you can see reflected in almost every popular book and article, down to the present -- the subject acquired an undeserved reputation for being hard. Educated people memorized the slogans -- "light is both a wave and a particle," "the cat is neither dead nor alive until you look," "you can ask about the position or the momentum, but not both," "one particle instantly learns the spin of the other through spooky action-at-a-distance," etc. -- and also learned that they shouldn't even try to understand such things without years of painstaking work.
The second way to teach quantum mechanics leaves a blow-by-blow account of its discovery to the historians, and instead starts directly from the conceptual core -- namely, a certain generalization of probability theory to allow minus signs. Once you know what the theory is actually about, you can then sprinkle in physics to taste, and calculate the spectrum of whatever atom you want. This second approach is the one I'll be following here.
So, what is quantum mechanics? Even though it was discovered by physicists, it's not a physical theory in the same sense as electromagnetism or general relativity. In the usual "hierarchy of sciences" -- with biology at the top, then chemistry, then physics, then math -- quantum mechanics sits at a level between math and physics that I don't know a good name for. Basically, quantum mechanics is the operating system that other physical theories run on as application software (with the exception of general relativity, which hasn't yet been successfully ported to this particular OS). There's even a word for taking a physical theory and porting it to this OS: "to quantize."
But if quantum mechanics isn't physics in the usual sense -- if it's not about matter, or energy, or waves, or particles -- then what is it about? From my perspective, it's about information and probabilities and observables, and how they relate to each other.
Scott: Yes, it is.
My contention in this lecture is the following: Quantum mechanics is what you would inevitably come up with if you started from probability theory, and then said, let's try to generalize it so that the numbers we used to call "probabilities" can be negative numbers. As such, the theory could have been invented by mathematicians in the 19th century without any input from experiment. It wasn't, but it could have been.
Scott: Yes -- and to me, that's a perfect illustration of why experiments are relevant in the first place! More often than not, the only reason we need experiments is that we're not smart enough. After the experiment has been done, if we've learned anything worth knowing at all, then hopefully we've learned why the experiment wasn't necessary to begin with -- why it wouldn't have made sense for the world to be any other way. But we're too dumb to figure it out ourselves!
Two other perfect examples of "obvious-in-retrospect" theories are evolution and special relativity. Admittedly, I don't know if the ancient Greeks, sitting around in their togas, could have figured out that these theories were true. But certainly -- certainly! -- they could've figured out that they were possibly true: that they're powerful principles that would've at least been on God's whiteboard when She was brainstorming the world.
In this lecture, I'm going to try to convince you -- without any recourse to experiment -- that quantum mechanics would also have been on God's whiteboard. I'm going to show you why, if you want a universe with certain very generic properties, you seem forced to one of three choices: (1) determinism, (2) classical probabilities, or (3) quantum mechanics. Even if the "mystery" of quantum mechanics can never be banished entirely, you might be surprised by just how far people could've gotten without leaving their armchairs! That they didn't get far until atomic spectra and so on forced the theory down their throats is one of the strongest arguments I know for experiments being necessary.
A Less Than 0% Chance
Alright, so what would it mean to have "probability theory" with negative numbers? Well, there's a reason you never hear the weather forecaster talk about a -20% chance of rain tomorrow -- it really does make as little sense as it sounds. But I'd like you to set any qualms aside, and just think abstractly about an event with N possible outcomes. We can express the probabilities of those events by a vector of N real numbers:
Mathematically, what can we say about this vector? Well, the probabilities had better be nonnegative, and they'd better sum to 1. We can express the latter fact by saying that the 1-norm of the probability vector has to be 1. (The 1-norm just means the sum of the absolute values of the entries.)
But the 1-norm is not the only norm in the world -- it's not the only way we know to define the "size" of a vector. There are other ways, and one of the recurring favorites since the days of Pythagoras has been the 2-norm or Euclidean norm. Formally, the Euclidean norm means the square root of the sum of the squares of the entries. Informally, it means you're late for class, so instead of going this way and then that way, you cut across the grass.
Now, what happens if you try to come up with a theory that's like probability theory, but based on the 2-norm instead of the 1-norm? I'm going to try to convince you that quantum mechanics is what inevitably results.
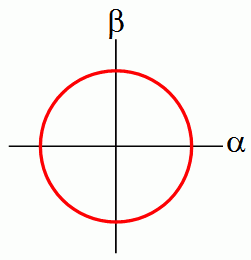
Let's consider a single bit. In probability theory, we can describe a bit as having a probability p of being 0, and a probability 1-p of being 1. But if we switch from the 1-norm to the 2-norm, now we no longer want two numbers that sum to 1, we want two numbers whose squares sum to 1. (I'm assuming we're still talking about real numbers.) In other words, we now want a vector (α,β) where α2 + β2 = 1. Of course, the set of all such vectors forms a circle:

The theory we're inventing will somehow have to connect to observation. So, suppose we have a bit that's described by this vector (α,β). Then we'll need to specify what happens if we look at the bit. Well, since it is a bit, we should see either 0 or 1! Furthermore, the probability of seeing 0 and the probability of seeing 1 had better add up to 1. Now, starting from the vector (α,β), how can we get two numbers that add up to 1? Simple: we can let α2 be the probability of a 0 outcome, and let β2 be the probability of a 1 outcome.
But in that case, why not forget about α and β, and just describe the bit directly in terms of probabilities? Ahhhhh. The difference comes in how the vector changes when we apply an operation to it. In probability theory, if we have a bit that's represented by the vector (p,1-p), then we can represent any operation on the bit by a stochastic matrix: that is, a matrix of nonnegative real numbers where every column adds up to 1. So for example, the "bit flip" operation -- which changes the probability of a 1 outcome from p to 1-p -- can be represented as follows:
Indeed, it turns out that a stochastic matrix is the most general sort of matrix that always maps a probability vector to another probability vector.
Exercise 1 for the Non-Lazy Reader: Prove this.
But now that we've switched from the 1-norm to the 2-norm, we have to ask: what's the most general sort of matrix that always maps a unit vector in the 2-norm to another unit vector in the 2-norm?
Well, we call such a matrix a unitary matrix -- indeed, that's one way to define what a unitary matrix is! (Oh, all right. As long as we're only talking about real numbers, it's called an orthogonal matrix. But same difference.) Another way to define a unitary matrix, again in the case of real numbers, is as a matrix whose inverse equals its transpose.
Exercise 2 for the Non-Lazy Reader: Prove that these two definitions are equivalent.
Scott: I'm gettin' to it -- don't you worry about that!
This "2-norm bit" that we've defined has a name, which as you know is qubit. Physicists like to represent qubits using what they call "Dirac ket notation," in which the vector (α,β) becomes . Here α is the amplitude of outcome |0〉, and β is the amplitude of outcome |1〉.
This notation usually drives computer scientists up a wall when they first see it -- especially because of the asymmetric brackets! But if you stick with it, you see that it's really not so bad. As an example, instead of writing out a vector like (0,0,3/5,0,0,0,4/5,0,0), you can simply write , omitting all of the 0 entries.
So given a qubit, we can transform it by applying any 2-by-2 unitary matrix -- and that leads already to the famous effect of quantum interference. For example, consider the unitary matrix
which takes a vector in the plane and rotates it by 45 degrees counterclockwise. Now consider the state |0〉. If we apply U once to this state, we'll get -- it's like taking a coin and flipping it. But then, if we apply the same operation U a second time, we'll get |1〉:
So in other words, applying a "randomizing" operation to a "random" state produces a deterministic outcome! Intuitively, even though there are two "paths" that lead to the outcome |0〉, one of those paths has positive amplitude and the other has negative amplitude. As a result, the two paths interfere destructively and cancel each other out. By contrast, the two paths leading to the outcome |1〉 both have positive amplitude, and therefore interfere constructively.
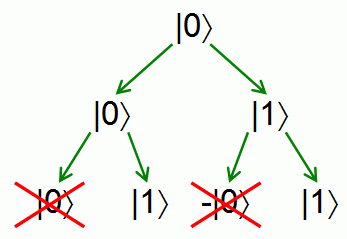
The reason you never see this sort of interference in the classical world is that probabilities can't be negative. So, cancellation between positive and negative amplitudes can be seen as the source of all "quantum weirdness" -- the one thing that makes quantum mechanics different from classical probability theory. How I wish someone had told me that when I first heard the word "quantum"!
Mixed States
Once we have these quantum states, one thing we can always do is to take classical probability theory and "layer it on top." In other words, we can always ask, what if we don't know which quantum state we have? For example, what if we have a 1/2 probability of and a 1/2 probability of
? This gives us what's called a mixed state, which is the most general kind of state in quantum mechanics.
Mathematically, we represent a mixed state by an object called a density matrix. Here's how it works: say you have this vector of N amplitudes, (α1,...,αN). Then you compute the outer product of the vector with itself -- that is, an N-by-N matrix whose (i,j) entry is αiαj (again in the case of real numbers). Then, if you have a probability distribution over several such vectors, you just take a linear combination of the resulting matrices. So for example, if you have probability p of some vector and probability 1-p of a different vector, then it's p times the one matrix plus 1-p times the other.
The density matrix encodes all the information that could ever be obtained from some probability distribution over quantum states, by first applying a unitary operation and then measuring.
Exercise 3 for the Non-Lazy Reader: Prove this.
This implies that if two distributions give rise to the same density matrix, then those distributions are empirically indistinguishable, or in other words are the same mixed state. As an example, let's say you have the state with 1/2 probability, and
with 1/2 probability. Then the density matrix that describes your knowledge is
It follows, then, that no measurement you can ever perform will distinguish this mixture from a 1/2 probability of |0〉 and a 1/2 probability of |1〉.
The Squaring Rule
Now let's talk about the question Gus raised, which is, why do we square the amplitudes instead of cubing them or raising them to the fourth power or whatever?
Scott: Yeah, you do want an answer that agrees with experiment. So let me put the question differently: why did God choose to do it that way and not some other way?
Ray Laflamme: Well, given that the numbers can be negative, squaring them just seems like the simplest thing to do!
Scott: Why not just take the absolute value?
Alright, I can give you a couple of arguments for why God decided to square the amplitudes.
The first argument is a famous result called Gleason's Theorem from the 1950's. Gleason's Theorem lets us assume part of quantum mechanics and then get out the rest of it! More concretely, suppose we have some procedure that takes as input a unit vector of real numbers, and that spits out the probability of an event. Formally, we have a function f that maps a unit vector to the unit interval [0,1]. And let's suppose N=3 -- the theorem actually works in any number of dimensions three or greater (but interestingly, not in two dimensions). Then the key requirement we impose is that, whenever three vectors v1,v2,v3 are all orthogonal to each other,
Intuitively, if these three vectors represent "orthogonal ways" of measuring a quantum state, then they should correspond to mutually-exclusive events. Crucially, we don't need any assumption other than that -- no continuity, no differentiability, no nuthin'.
So, that's the setup. The amazing conclusion of the theorem is that, for any such f, there exists a mixed state such that f arises by measuring that state according to the standard measurement rule of quantum mechanics. I won't be able prove this theorem here, since it's pretty hard. But it's one way that you can "derive" the squaring rule without exactly having to put it in at the outset.
Exercise 4 for the Non-Lazy Reader: Why does Gleason's Theorem not work in two dimensions?
If you like, I can give you a much more elementary argument. This is something I put it in one of my papers, though I'm sure many others knew it before.
Let's say we want to invent a theory that's not based on the 1-norm like classical probability theory, or on the 2-norm like quantum mechanics, but instead on the p-norm for some . Call (v1,...,vN) a unit vector in the p-norm if
Then we'll need some "nice" set of linear transformations that map any unit vector in the p-norm to another unit vector in the p-norm.
It's clear that for any p we choose, there will be some linear transformations that preserve the p-norm. Which ones? Well, we can permute the basis elements, shuffle them around. That'll preserve the p-norm. And we can stick in minus signs if we want. That'll preserve the p-norm too. But here's the little observation I made: if there are any linear transformations other than these trivial ones that preserve the p-norm, then either p=1 or p=2. If p=1 we get classical probability theory, while if p=2 we get quantum mechanics.
Scott: Exactly! Then you have to set p=1 or p=2.
Exercise 5 for the Non-Lazy Reader: Prove my little observation.
Alright, to get you started, let me give some intuition about why my observation might be true. Let's assume, for simplicity, that everything is real and that p is a positive even integer (though the observation also works with complex numbers and with any real p≥0). Then for a linear transformation A=(aij) to preserve the p-norm means that
whenever
Now we can ask: how many constraints are imposed on the matrix A by the requirement that this be true for every v1,...,vN? If we work it out, in the case p=2 we'll find that there are constraints. But since we're trying to pick an N-by-N matrix, that still leaves us N(N-1)/2 degrees of freedom to play with.
On the other hand, if (say) p=4, then the number of constraints grows like , which is greater than N2 (the number of variables in the matrix). That suggests that it will be hard to find a nontrivial linear transformation that preserves 4-norm. Of course it doesn't prove that no such transformation exists -- that's left as a puzzle for you.
Incidentally, this isn't the only case where we find that the 1-norm and 2-norm are "more special" than other p-norms. So for example, have you ever seen the following equation?
There's a cute little fact -- unfortunately I won't have time to prove it in class -- that the above equation has nontrivial integer solutions when n=1 or n=2, but not for any larger integers n. Clearly, then, if we use the 1-norm and the 2-norm more than other vector norms, it's not some arbitrary whim -- these really are God's favorite norms! (And we didn't even need an experiment to tell us that.)
Real vs. Complex Numbers
Even after we've decided to base our theory on the 2-norm, we still have at least two choices: we could let our amplitudes be real numbers, or we could let them be complex numbers. We know the solution God chose: amplitudes in quantum mechanics are complex numbers. This means that you can't just square an amplitude to get a probability; first you have to take the absolute value, and then you square that. In other words, if the amplitude for some measurement outcome is α = β + γi, where β and γ are real, then the probability of seeing the outcome is |α|2 = β2 + γ2.
Why did God go with the complex numbers and not the real numbers?
Years ago, at Berkeley, I was hanging out with some math grad students -- I fell in with the wrong crowd -- and I asked them that exact question. The mathematicians just snickered. "Give us a break -- the complex numbers are algebraically closed!" To them it wasn't a mystery at all.
But to me it is sort of strange. I mean, complex numbers were seen for centuries as fictitious entities that human beings made up, in order that every quadratic equation should have a root. (That's why we talk about their "imaginary" parts.) So why should Nature, at its most fundamental level, run on something that we invented for our convenience?
Scott: Dammit, you're getting ahead of me!
Alright, yeah: suppose we require that, for every linear transformation U that we can apply to a state, there must be another transformation V such that V2 = U. This is basically a continuity assumption: we're saying that, if it makes sense to apply an operation for one second, then it ought to make sense to apply that same operation for only half a second.
Can we get that with only real amplitudes? Well, consider the following linear transformation:
This transformation is just a mirror reversal of the plane. That is, it takes a two-dimensional Flatland creature and flips it over like a pancake, sending its heart to the other side of its two-dimensional body. But how do you apply half of a mirror reversal without leaving the plane? You can't! If you want to flip a pancake by a continuous motion, then you need to go into ... dum dum dum ... THE THIRD DIMENSION.
More generally, if you want to flip over an N-dimensional object by a continuous motion, then you need to go into the (N+1)st dimension.
Exercise 6 for the Non-Lazy: Prove that any norm-preserving linear transformation in N dimensions can be implemented by a continuous motion in N+1 dimensions.
But what if you want every linear transformation to have a square root in the same number of dimensions? Well, in that case, you have to allow complex numbers. So that's one reason God might have made the choice She did.
Alright, I can give you two other reasons why amplitudes should be complex numbers.
The first comes from asking, how many independent real parameters are there in an N-dimensional mixed state? As it turns out, the answer is exactly N2 -- provided we assume, for convenience, that the state doesn't have to be normalized (i.e., that the probabilities can add up to less than 1). Why? Well, an N-dimensional mixed state is represented mathematically by a N-by-N Hermitian matrix with positive eigenvalues. Since we're not normalizing, we've got N independent real numbers along the main diagonal. Below the main diagonal, we've got N(N-1)/2 independent complex numbers, which means N(N-1) real numbers. Since the matrix is Hermitian, the complex numbers below the main diagonal determine the ones above the main diagonal. So the total number of independent real parameters is N + N(N-1) = N2.
Now we bring in an aspect of quantum mechanics that I didn't mention before. If we know the states of two quantum systems individually, then how do we write their combined state? Well, we just form what's called the tensor product. So for example, the tensor product of two qubits, α|0〉+β|1〉 and γ|0〉+δ|1〉, is given by
Again one can ask: did God have to use the tensor product? Could She have chosen some other way of combining quantum states into bigger ones? Well, maybe someone else can say something useful about this question -- I have trouble even wrapping my head around it! For me, saying we take the tensor product is almost what we mean when we say we're putting together two systems that exist independently of each other.
As you all know, there are two-qubit states that can't be written as the tensor product of one-qubit states. The most famous of these is the EPR (Einstein-Podolsky-Rosen) pair:
Given a mixed state ρ on two subsystems A and B, if ρ can be written as a probability distribution over tensor product states , then we say ρ is separable. Otherwise we say ρ is entangled.
Now let's come back to the question of how many real parameters are needed to describe a mixed state. Suppose we have a (possibly-entangled) composite system AB. Then intuitively, it seems like the number of parameters needed to describe AB -- which I'll call dAB -- should equal the product of the number of parameters needed to describe A and the number of parameters needed to describe B:
If amplitudes are complex numbers, then happily this is true! Letting NA and NB be the number of dimensions of A and B respectively, we have
But what if the amplitudes are real numbers? In that case, in an N-by-N density matrix, we'd only have N(N+1)/2 independent real parameters. And it's not the case that if N = NA NB then
Scott: Excellent question. Yes! With real numbers the left-hand side is too big, whereas with quaternions it's too small. Only with complex numbers is it juuuuust right!
There's actually another phenomenon with the same "Goldilocks" flavor, which was observed by Bill Wootters -- and this leads to my third reason why amplitudes should be complex numbers. Let's say we choose a quantum state
uniformly at random (if you're a mathematician, under the Haar measure). And then we measure it, obtaining outcome |i〉 with probability |αi|2. The question is, will the resulting probability vector also be distributed uniformly at random in the probability simplex? It turns out that if the amplitudes are complex numbers, then the answer is yes. But if the amplitudes are real numbers or quaternions, then the answer is no! (I used to think this fact was just a curiosity, but now I'm actually using it in a paper I'm working on...)
Linearity
We've talked about why the amplitudes should be complex numbers, and why the rule for converting amplitudes to probabilities should be a squaring rule. But all this time, the elephant of linearity has been sitting there undisturbed. Why would God have decided, in the first place, that quantum states should evolve to other quantum states by means of linear transformations?
Scott: Close! Steven Weinberg and others proposed nonlinear variants of quantum mechanics in which the state vectors do stay the same size. The trouble with these variants is that they'd let you take far-apart vectors and squash them together, or take extremely close vectors and pry them apart! Indeed, that's essentially what it means for such theories to be nonlinear. So our configuration space no longer has this intuitive meaning of measuring the distinguishability of vectors. Two states that are exponentially close might in fact be perfectly distinguishable. And indeed, in 1998 Abrams and Lloyd used exactly this observation to show that, if quantum mechanics were nonlinear, then one could build a computer to solve NP-complete problems in polynomial time.
Question: What's the problem with that?
Scott: What's the problem with being able to solve NP-complete problems in polynomial time? Oy, if by the end of this class you still don't think that's a problem, I will have failed you... [laughter]
Seriously, of course we don't know whether NP-complete problems are efficiently solvable in the physical world. But in a survey I wrote a couple years ago, I explained why the ability to solve NP-complete problems would give us "godlike" powers -- arguably, even more so than the ability to transmit superluminal signals or reverse the Second Law of Thermodynamics. The basic point is that, when we talk about NP-complete problems, we're not just talking about scheduling airline flights (or for that matter, breaking the RSA cryptosystem). We're talking about automating insight: proving the Riemann Hypothesis, modeling the stock market, seeing whatever patterns or chains of logical deduction are there in the world to be seen.
So, suppose I maintain the working hypothesis that NP-complete problems are not efficiently solvable by physical means, and that if a theory suggests otherwise, more likely than not that indicates a problem with the theory. Then there are only two possibilities: either I'm right, or else I'm a god! And either one sounds pretty good to me...
Exercise 7 for the Non-Lazy Reader: Prove that if quantum mechanics were nonlinear, then not only could you solve NP-complete problems in polynomial time, you could also use EPR pairs to transmit information faster than the speed of light.
Scott: Yeah, you've touched on another one of my favorite questions: why should the speed of light be finite? Well, one reason I'd like it to be finite is that, if aliens from the Andromeda galaxy are going to hurt me, then I at least want them to have to come here first!
Further Reading
See this paper by Lucien Hardy for a "derivation" of quantum mechanics that's closely related to the arguments I gave, but much, much more serious and careful. Also see pretty much anything Chris Fuchs has written (and especially this paper by Caves, Fuchs, and Schack, which discusses why amplitudes should be complex numbers rather than reals or quaternions).
[Discussion of this lecture on blog]