PHYS771 Lecture 20: Cosmology and Complexity

Scott Aaronson

Scribe: Chris Granade

Puzzle from last week: What can you compute with "narrow" CTCs that only send one bit back in time?

Solution: Let x be a chronology-respecting bit, and let y be a CTC bit. Then, set x := x ⊕ y and y := x. Suppose that Pr[x = 1] = p and Pr[y = 1] = q. Then, causal consistency implies p = q. Hence, Pr[x ⊕ y = 1] = p(1 − q) + q(1 − p) = 2p(1 − p).

So we can start with p exponentially small, and then repeatedly amplify it. We can thereby solve NP-complete problems in polynomial time (and indeed PP ones also, provided we have a quantum computer).

I was going to offer some grand summation that would drive home the central message of this class, but then I thought about it and realized that there is no central message. I just stand up here and rant about whatever I deem interesting. What we'll do instead is to talk about cosmology and complexity.

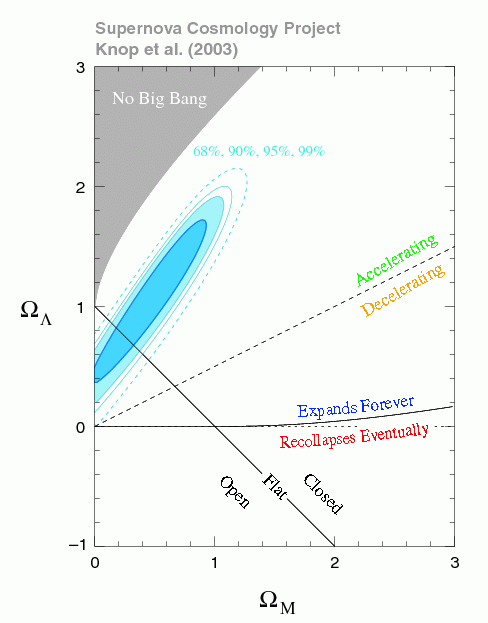
I'll start with the "New York Times model" of cosmology– that is, the thing that you read about in popular articles until fairly recently– which says that everything depends on the density of matter in the universe. There's this parameter Ω which represents the mass density of the universe, and if it's greater than 1, the universe is closed. That is, the matter density of the universe is high enough that after the Big Bang, there has to be a Big Crunch. Furthermore, if Ω>1, spacetime has a spherical geometry (positive curvature). If Ω=1, the geometry of spacetime is flat and there's no Big Crunch. If Ω<1, then the universe is open, and has a hyperbolic geometry. The view was that these are the three cases.

Today, we know that this model is wrong in at least two ways. The first way it's wrong is of course that it ignores the cosmological constant. As far as astronomers can see, space is roughly flat. That is, no one has detected a non-trivial spacetime curvature at the scale of the universe. There could be some curvature, but if there is, then it's pretty small. The old picture would therefore lead you to think that the universe must be poised on the brink of a Big Crunch: change the matter density just a tiny bit, and you could get a spherical universe that collapses or a hyperbolic one that expands forever. But in fact, the universe is not anywhere near the regime where there would be a Big Crunch. Why are we safe? Well, you have to look at what the energy density of the universe is made up of. There's matter, including ordinary matter as well as dark matter, there's radiation, and then there's the famous cosmological constant detected a decade ago, which describes the energy density of empty space. Their (normalized) sum Ω seems to equal 1 as far as anyone can measure, which is what makes space flat, but the cosmological constant Λ is not zero, as had been assumed for most of the 20^th century. In fact, about 70% of the energy density of the observable universe (in this period of time) is due to the cosmological constant.

From http://www-supernova.lbl.gov/.

Along the diagonal black line is where space is flat. This is where the energy densities due to the cosmological constant and matter sum to 1. In the previous view, there was no cosmological constant, and space was flat, and so we're at the intersection of the two solid black lines. You can see the other solid black line slowly starts curving up. If you're above that line, then the universe expands forever, whereas if you're below this line, then the universe recollapses. So if you're at the intersection, then you really are right at the brink between expanding and collapsing. But, given that 70% of the energy density of the universe is due to Λ, you can see that we're somewhere around the intersection of the diagonal line with the blue oval–i.e., nowhere near where we recollapse.

But that's only one thing that's wrong with the simple "spherical/flat/hyperbolic" trichotomy. Another thing wrong with it is that the geometry of the universe and its topology are two separate questions. Just assuming the universe is flat doesn't imply that it's infinite. If the universe had a constant positive curvature, that would imply it was finite. Picture the Earth; on learning that it has a constant positive curvature, you would conclude it's round. I mean, yes, it could curve off to infinity where you can't see it, but assuming it's homogenous in curvature, mathematically it has to curve around in either a sphere or some other more complicated finite shape. If space is flat, however, that doesn't tell you whether it's is finite or infinite. It could be like one of the video games where when you go off one end of the screen, you reappear on the other end. That's perfectly compatible with geometric flatness, but would correspond to a closed topology. The answer, then, to whether the universe is finite or infinite, is unfortunately that we don't know. (For more see this paper by Cornish and Weeks.)

Q: But with positive curvature, you could have something that tapers off infinitely like a paraboloid.
Scott: Yes, but that wouldn't be uniform positive curvature. Uniform means that the curvature is the same everywhere.
Q: It seems like what's missing in all these pictures so far is time. Are we saying that time started at some fixed point, or that time goes all the way back to negative infinity?
Scott: All of these pictures assume that there was a Big Bang, right? All of these are Big Bang cosmologies.
Q: So if time started at some finite point, then time is finite. But relativity tells us that there's really no difference between space and time, right?
Scott: No, it doesn't tell us that. It tells us that time and space are interrelated in a non-trivial way, but time has a different metric signature than space. As an aside, this is one of my pet peeves. I actually had a physicist ask me once how P could be different from PSPACE since "relativity tells us that time and space are the same." Well, the point is that time has a negative signature. This is related to the fact that you can go backwards and forwards in space, but you can only go forwards in time. We talked in the last lecture about closed timelike curves. The point about CTCs is that they would let you go backwards in time and as a consequence, time and space really would become equivalent as computational resources. But as long as you can only go one direction in time, it's not the same as space.
Q: So can we go far in space enough to loop around?
Scott: If your arm was long enough, could you stretch it out in front of you and punch yourself in the back of your head? As I was saying, the answer is that we don't know.
Q: As far as the spread of mass is concerned, I think that people believe that is finite, because of the Big Bang.
Scott: That's a misconception about the Big Bang. The Big Bang is not something that happens at one point in space; the Big Bang is the event that creates spacetime itself. The standard analogy is that the galaxies are little spots on a balloon, and as the balloon expands, it's not that the spots are rushing away from each other, it's that the balloon is getting bigger. If spacetime is open, then it could well be that instead of just having a bunch of matter crowded around, you've actually got an infinite amount of matter at the moment of the Big Bang. As time goes by, the infinite universe gets stretched out, but at any point in time, it would still go on infinitely. If you look at our local horizon, we see things rushing away from each other, but that's just because we can't go past that horizon and see what's beyond it. So the Big Bang isn't some explosion that happened at some time and place; it's just the beginning of the whole manifold.
Q: But then shouldn't the mass/energy not spread out faster than the speed of light?
Scott: That's another great question; I'm glad to have something I can actually explain! Within a fixed reference frame, you can have two points appearing to recede from each other faster than light, but the reason is they appear to recede is just that the intervening space is expanding. Indeed, the empirical fact is that faraway galaxies do rush away from each other faster than light. What's limited by the speed of light is the speed with which an ant can move along the surface of the expanding balloon--not the expansion speed of the balloon itself.
Q: So would it be possible to observe an object moving away faster than the speed of light?
Scott: Well, if some light was emitted a long time ago (say, shortly after the Big Bang), then by the time that light reaches us, we may be able to infer that the galaxy the light came from must now be receding away from us faster than the speed of light.
Q: Can two galaxies move towards each other faster than the speed of light?
Scott: In a collapse, yes.
Q: How do we avoid all the old paradoxes that come with allowing objects to move faster than the speed of light?
Scott: In other words, why doesn't faster-than-light expansion or contraction cause causality problems? See, this is where I start having to defer to people who actually understand GR. But let me take a shot: there are certainly possible geometries of spacetime–for example, those involving wormholes, or Gödel's rotating universe–that do have causality problems. But what about the actual geometry we live in? Here, things are just receding away from each other, which is not something you can actually use to sendsignals faster than light. What you can get, in our geometry, are objects that are so far away from each other that naïvely they should "never have been in causal contact," but nevertheless seem like they must have been. So, the hypothesis is that there was a period of rapid inflation in the extremely early universe, so that objects could reach equilibrium with each other and only then be causally separated by inflation.

So what is this cosmological constant? Basically, a kind of anti-gravity. It's something that causes two given points in spacetime to recede away from each other at an exponential rate. What's the obvious problem with that? As the Woody Allen character's mother told him, "Brooklyn is not expanding." If this expansion is such an important force in the universe, why doesn't it matter within our own planet or galaxy? Because on the scale that we live, there are other forces like gravity that are constantly counteracting the expansion. Imagine two magnets on the surface of a slowly-expanding balloon: even though the balloon is expanding, the magnets still stick together. It's only on the scale of the entire universe that the cosmological constant is able to win over gravity.

You can talk about this in terms of the scale factor of the universe. Let's measure the time t since the beginning of the universe in the rest frame of the cosmic background radiation (the usual trick). How "big" is the universe as a function of t? Or to put it more carefully, given two test points, how has the distance between them changed as a function of time? The hypothesis behind inflation is that at the very beginning–at the Big Bang–there's this enormous exponential growth for a few Planck times. Following that, you've got some expansion, but also have gravity trying to pull the universe together. It works out there that the scale factor increases as t^2/3. Ten billion years after the Big Bang, when life is first starting to form on Earth, the cosmological constant starts winning out over gravity. After this, it's just exponential all the way, like in the very beginning but not as fast.

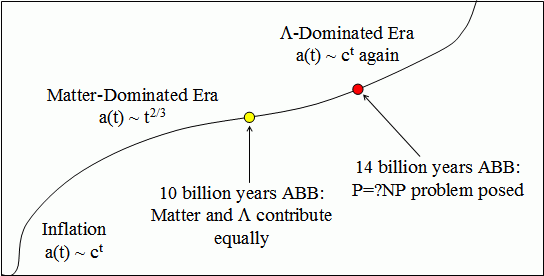
Evolution of the scale factor a(t) (not to scale).

So that's how physicists would describe the cosmological constant, but how I would describe it is just the inverse of the number of bits that can ever be used in a computation! More precisely:

Q: What's the definition of the cosmological constant?
Scott: It's the vacuum energy. Again, this is physics. People don't define things, they observe them. They don't actually know what this vacuum energy is, they just know it's there. It's an energy of empty space, and could have many different possible origins.
Q: An average?
Scott: Well, yes, but it seems to be very close to constant wherever people can measure it and also seems to be very constant over time. No one has found any deviation from the assumption that it's the same everywhere. One way to think of it is that, in a vacuum, there's always these particle/anti-particle pairs forming and annihilating each other. Empty space is an extremely complicated thing! So maybe it's not so surprising that it should have a non-zero energy. Indeed, the hard problem in quantum field theory is not to explain why there's a cosmological constant, but rather to explain why it isn't 10¹²⁰ times larger than it is! A naïve quantum field theory argument gives you a prediction that the entire universe should just blow apart in an instant.
Q: So is this Ω_Λ?
Scott: No, Ω_Λ is the fraction of the total energy density that's comprised of the cosmological constant. So that also depends on the matter density, and unlike Λ itself it can change with time.

To see what any of this has to do with computation, we have to take a detour into the holographic bound. This is one of the few things that seems to be known about quantum gravity, with the string theorists and loop quantum gravity people actually agreeing. Plus it's a bound, which is a language I speak. My treatment will follow a nice survey paper by Bousso. I'm going to make this assigned reading, but only for the physicists. We saw way back in the first lecture that there's this Planck area ℓ_p² = Gℏ/c³. You can get it by combining a bunch of physical constants together until the units cancel such that you get length². Planck himself did that back around 1900. This is clearly very deep, because you're throwing together Newton's constant, Planck's constant and the speed of light and you're getting a length scale which is on the order of 10^-69 m².

The holographic bound says that in any region of spacetime, the amount of entropy that you can put in the region–or up to a small constant, the number of bits you can store in it–is at most the surface area of the region measured in Planck units divided by 4. This is the surprising part: the number of bits you can store doesn't grow with the volume, it grows with the surface area. I can show you a derivation of this (or rather, what the physicists take to be a derivation).

Q: Does the derivation tell you why you divide by 4 and not, say, 3?
Scott: The string theorists believe they have an explanation of that. It's one big success that they like to lord over other quantum gravity approaches! For the loop quantum gravity people, the constant comes out wrong and they have to adjust it by hand by what they call the Immirzi parameter.

The rough intuition is that if you try to build a cube of bits (say, a hard disk) and keep making it bigger and bigger, then it's eventually going to collapse to a black hole. At that point, you can still put more bits in it, but when you do that, the information just sort of gloms onto the event horizon in a way that people don't fully understand. But however it happens, from that point on, the information content is just going to increase like the surface area.

To "derive" this, the first ingredient we need is the so-called Bekenstein bound. Bekenstein was the guy who back in the 70s realized that black holes should have an entropy. Why? If there's no entropy and you drop something into a black hole, it disappears, which would seem to violate the Second Law of Thermodynamics. Furthermore, black holes exhibit all sorts of unidirectional properties: you can drop something in a black hole but you can't get it out, or you can merge two black holes and get a bigger one but then you can't split one black hole into multiple smaller black holes. This unidirectionality is extremely reminiscent of entropy. This is obvious in retrospect; even someone like me can see it in retrospect.

So what is this Bekenstein bound? It says that in Planck units, the entropy S of any given region satisfies:

Q: Doesn't the area go like the square of the radius?
Scott: It does.
Q: Then why should R appear in the Bekenstein bound and not R²?
Scott: We're getting to that!

That's fact one. Fact two is the Schwarzschild bound, which says that the energy of a system can be at most proportional to its radius. In Planck units, E ≤ R/2. This is again because if you were to pack matter/energy more densely than that, it would eventually collapse to a black hole. If you want to build a hard disk where each bit takes a fixed amount of energy to represent, then you can make a one-dimensional Turing tape which could go on indefinitely, but if you tried to make it even two-dimensional, then when it became big enough, it would collapse to a black hole. The radius of a black hole is proportional to its mass (its energy) by this relationship. You could say that a black hole gives you the most bang for your buck in terms of having the most energy in a given radius. So black holes are maximal in at least two senses: they have the most energy per radius and also the most entropy per radius.

Now, if you accept these two facts, then you can put them together:

There actually is a problem with the holographic bound as I've stated it—it clearly fails in some cases. One of them would be a closed spacetime. Let's say that space is closed—if you go far enough in one direction you appear back in another direction—and let's say that this region here can be at most proportional to the surface area. But how do I know that this is the inside? There's a joke where a farmer hires a mathematician to build a fence in as efficient a fashion as possible–that is, to build a fence with the most area inside given some perimeter. So the mathematician builds a tiny circle of fence, steps inside and declares the rest of the Earth to be outside. Maybe the whole rest of the universe is the inside! Clearly, the amount of entropy in the entire rest of the universe could be more than the surface area of this tiny little black hole, or whatever else it is. In general, the problem with the holographic bound is that it is not "relativistically covariant." You could have the same surface area, and in one reference frame, the holographic bound is true, whereas in another it might fail.

Anyway, it appears that Bousso and others have essentially solved these problems. The way they do it is by looking at "null hypersurfaces," which are made up of paths traced by photons (geodesics). These are relativistically invariant. So the idea is that you have some region, and you look at the light rays emanating from the surface of the region. Then, you define the inside of the region to be the direction in which the light rays are converging upon each other. One advantage of doing it this way is that you can switch to another reference frame, but these geodesics are unchanged. On this account, the way you should interpret the holographic bound is as upper bounding the amount of entropy you could see in the region if you could travel from the surface inwards at the speed of light. In other words, the entropy being upper-bounded is the entropy you would see along these null hypersurfaces. Doing it this way seems to solve the problems.

So what does any of this have to do with computation? You might say that if the universe is infinite, then clearly, in principle you could perform an arbitrarily long computation. You just need enough Turing machine tape. What's the problem with that argument?

Q: The tape would collapse to a black hole?
Scott: As I said, you could just have a one-dimensional tape, and that could be extended arbitrarily.
Q: What if the tape starts receding away from you?
Scott: Right! Your bits are right there, then after you turn your back for just a few tens of billions of years, they've receded beyond your cosmological horizon due to the expansion of the universe.

The point is, it's not enough just to have all of these bits available in the universe somewhere. You have to be able to control all of them—you have to be able to set them all—and then you need to be able to access them later while performing a computation. Bousso formalizes this notion with what he calls a "causal diamond," but I'd just call it a computation with an input and an output. The idea is you have some starting point P and some endpoint Q, and then you look at the intersection of the forward light-cone of P and the past light-cone of Q. That's a causal diamond. The idea is that for any experiment we could actually perform—any computation we could actually do—we're going to have to have some starting point of the experiment, and some end point where you collect the data (read the output). What's relevant isn't the total amount of entropy in the universe, but just the total amount of entropy that can be contained in one of these causal diamonds. So now, Bousso has this other paper where he argues that if you're in a de Sitter space—that is, a space with a cosmological constant, like the space we seem to live in—then, the amount of entropy that can be contained in one of these causal diamonds is at most 3π/Λ. That's why, in our universe, there's the bound of around 10¹²² bits. The point is that the universe is expanding at an exponential rate, and so a point that's at the edge of our horizon now will be, after another 15 billion years or so (another age of the universe), a constant factor as far away as it is now.

Q: So where do you place P and Q to get that number?
Scott: You could put them anywhere. You're maximizing over all P and Q. That's really the key point here.
Q: Then where does the maximum occur?
Scott: Well, pick P wherever you like, then pick Q maybe a couple tens of billion years in its causal future. If you don't wrap your computation up after 20 billion years or so, then the data at the other end of your memory is going to recede past your cosmological horizon. You can't actually build a working computer whose radius is more than 20 billion light years or whatever. It's depressing, but true.
Q: Does Λ change with time?
Scott: The prevailing belief is that it doesn't change with time. It might, but there are pretty strong experimental constraints on how much. Now the proportion Ω_Λ of the energy density taken up by Λ, that is changing. As the universe gets more and more dilute, the proportion of the energy taken up by Λ gets bigger and bigger, even though Λ itself stays the same.
Q: But the radius of the universe is changing.
Scott: Yes. In our current epoch, we get to see a larger and larger amount of the past as light reaches us from further and further away. But once Λ starts winning out over matter, the radius of the observable universe will reach a steady state of 10 billion light years or whatever it is.
Q: Why is it 10 billion light years?
Scott: Because that's the distance such that something that far away from you will appear to be receding away from you at the speed of light, if there's no countervailing influence of gravity.
Q: So it's just a coincidence that that distance happens to be about the current size of the observable universe?
Scott: Either a coincidence or something deeper that we don't fully understand yet!

This is fine, but I promised you that I'd talk about computational complexity. Well, if the holographic bound combined with the cosmological constant put a finite upper bound on the number of bits in any possible computation, then you might argue that we can only solve problems that are solvable in constant time! And you might feel that in some sense, this trivializes all of complexity theory. Fortunately, there's an elegant way out of that: we say that now we're interested in asymptotics not just in n (the size of the input), but in 1/Λ. Forget for now that Λ has a known (tiny) value, and think of it as a varying parameter—then complexity theory comes back! Taking that point of view, let me make the following claim: suppose the universe is (1+1)-dimensional (that is, one space and one time dimension) and has cosmological constant Λ. Then the class of problems that we can solve is contained in DSPACE(1/Λ): the class of problems solvable by a deterministic Turing machine using ~1/Λ tape squares. In fact it's equal to DSPACE(1/Λ), depending on what assumptions you want to make about the physics. Certainly it at least contains DSPACE(1/√Λ).

First of all, why can't we do more than DSPACE(1/Λ)?

Well, to be more formal, let me define a model of computation that I'll call the Cosmological Constant Turing Machine. In this model, you've got an infinite Turing machine tape, but now at every time step, between every two squares, there's an independent probability Λ of a new square forming with a '*' symbol in it. As a first pass, this seems like a reasonable model for how Λ would affect computation. Now, if your tape head is at some square, the squares at a distance 1/Λ will appear to be receding away from the tape head at a rate of one square per time step on average. So, you can't hope to ever journey to those squares. Every time you step towards them, a new square will probably be born in the intervening space. (You can think of the speed of light in this model as one tape square per time step.) So, the class of problems you can solve will be contained in DSPACE(1/Λ), since you can always just record the contents of the squares that are within 1/Λ of the current position of the tape head, and ignore the other squares.

But can we actually achieve DSPACE(1/Λ)? You might imagine a very simple algorithm for doing so. Namely, just think of your 1/Λ bits as a herd of cattle that keep wandering away from each other. You have to keep lassoing them together like a cosmological cowboy. In other words, your tape head will just keep going back and forth, compressing the bits together as they try to spread out while simultaneously performing the computation on them. Now, the question is, can you actually lasso the bits together in time O(1/Λ)? I haven't written out a proof of this, but I don't think it's possible in less than ~1/Λ² time with a standard Turing machine head (one without, e.g., the ability to delete tape squares). On the other hand, certainly you can lasso ~1/√Λ bits in O(1/Λ) time. You can therefore compute DSPACE(1/√Λ). I conjecture that this is tight.

A second interesting point is that in two or more dimensions, you don't get the same picture. In two dimensions, the radius still doubles on a timescale of about 1/Λ, but even to visit all the bits that need to be lassoed now takes on the order of 1/Λ² time. And so we can ask if there is something you can do on a 2-D square grid in time 1/Λ which you couldn't do in time 1/Λ on a 1-D tape. You've got this 1/Λ² space here, and intuitively you'd think that you can't make use of more than 1/Λ of the tape squares in 1/Λ time, but it's not clear if that's actually true. Of course, for added fun, you can also ask all of these questions for quantum Turing machines.

The other thing you can ask about is query complexity in this model. For example, what if you lost your keys and they could be anywhere in the universe? If your keys are somewhere within your cosmological horizon, and your space has one dimension, then in principle you can find them. You can traverse the entire space within your horizon in time O(1/Λ). But in two dimensions, the number of locations you can check before most of the observable universe has receded is only like the square root of the number of possible locations. You can pick some faraway place to go, take a journey there and by the time you come back, the region has doubled in size.

In the quantum case, there's actually a way out: use Grover's algorithm! Recall that Grover's algorithm lets us search a database of N items in only √N steps. So it would seem that this would let us search a 2-D database of size on the order of the observable universe. But there's a problem. Think about how Grover's algorithm actually works. You've got these query steps interleaved with the amplitude amplification steps. In order to amplify amplitudes, you've got to collect all the amplitudes in one place, so that you can perform the Grover reflection operation. If we think about some quantum robot searching a 2-D database having dimension √N × √N, then you only need to do √N iterations of Grover's algorithm, since there's only N items in the database, but each iteration takes √N time, since the robot has to gather the results of all the queries. That's a problem, because we don't seem to get any benefit over the classical case. Thus, the proposed solution for searching a database the size of the universe doesn't seem to work. It does seem to give us some advantage in three dimensions. If you think of a 3-D hard disk, here the side length is N^1/3, so we would need √N Grover iterations taking N^1/3 time each, giving a total time of N^5/6. At least that's somewhat better than N. As we add more dimensions, the performance would get closer to √N. For example, if space had 10 large dimensions, then we'd get a performance of N^12/22.

In a paper I wrote with Andris Ambainis some years ago, what we did is we showed that you can use a recursive variant of Grover's algorithm to search a 2-D grid using time of order √N log^3/2 N. For three or more dimensions, the time order is simply √N. I can give some very basic intuition as to how our algorithm works. What you do is use a divide-and-conquer strategy: that is, you divide your grid into a bunch of smaller grids. Then you can keep dividing the subgrid into smaller subgrids, and appoint regional Grover's algorithm commanders for each subgrid.

Even, as a first step, let's say that you search each row separately. Each row only takes √N time to search, and then you could come back and collect everything together. You can then do a Grover search of the √N rows, taking N^1/4 time, giving a total time of N^3/4.

That's the first way of solving the problem. Later, some other people discovered another way of doing it using quantum random walks, but the bottom line is that given a 2-D database the size of the universe, you actually can search it for a marked item before it recedes past the cosmological horizon. You can only do one search, or at best a constant number of searches, but at least you can find one thing you're really desperate for.

[Discussion of this lecture on blog]

[← Previous lecture | Next lecture →]

[Return to PHYS771 home page]