Common Knowledge and Aumann’s Agreement Theorem
The following is the prepared version of a talk that I gave at SPARC: a high-school summer program about applied rationality held in Berkeley, CA for the past two weeks. I had a wonderful time in Berkeley, meeting new friends and old, but I’m now leaving to visit the CQT in Singapore, and then to attend the AQIS conference in Seoul.
Common Knowledge and Aumann’s Agreement Theorem
August 14, 2015
Thank you so much for inviting me here! I honestly don’t know whether it’s possible to teach applied rationality, the way this camp is trying to do. What I know is that, if it is possible, then the people running SPARC are some of the awesomest people on earth to figure out how. I’m incredibly proud that Chelsea Voss and Paul Christiano are both former students of mine, and I’m amazed by the program they and the others have put together here. I hope you’re all having fun—or maximizing your utility functions, or whatever.
My research is mostly about quantum computing, and more broadly, computation and physics. But I was asked to talk about something you can actually use in your lives, so I want to tell a different story, involving common knowledge.
I’ll start with the “Muddy Children Puzzle,” which is one of the greatest logic puzzles ever invented. How many of you have seen this one?
OK, so the way it goes is, there are a hundred children playing in the mud. Naturally, they all have muddy foreheads. At some point their teacher comes along and says to them, as they all sit around in a circle: “stand up if you know your forehead is muddy.” No one stands up. For how could they know? Each kid can see all the other 99 kids’ foreheads, so knows that they’re muddy, but can’t see his or her own forehead. (We’ll assume that there are no mirrors or camera phones nearby, and also that this is mud that you don’t feel when it’s on your forehead.)
So the teacher tries again. “Knowing that no one stood up the last time, now stand up if you know your forehead is muddy.” Still no one stands up. Why would they? No matter how many times the teacher repeats the request, still no one stands up.
Then the teacher tries something new. “Look, I hereby announce that at least one of you has a muddy forehead.” After that announcement, the teacher again says, “stand up if you know your forehead is muddy”—and again no one stands up. And again and again; it continues 99 times. But then the hundredth time, all the children suddenly stand up.
(There’s a variant of the puzzle involving blue-eyed islanders who all suddenly commit suicide on the hundredth day, when they all learn that their eyes are blue—but as a blue-eyed person myself, that’s always struck me as needlessly macabre.)
What’s going on here? Somehow, the teacher’s announcing to the children that at least one of them had a muddy forehead set something dramatic in motion, which would eventually make them all stand up—but how could that announcement possibly have made any difference? After all, each child already knew that at least 99 children had muddy foreheads!
Like with many puzzles, the way to get intuition is to change the numbers. So suppose there were two children with muddy foreheads, and the teacher announced to them that at least one had a muddy forehead, and then asked both of them whether their own forehead was muddy. Neither would know. But each child could reason as follows: “if my forehead weren’t muddy, then the other child would’ve seen that, and would also have known that at least one of us has a muddy forehead. Therefore she would’ve known, when asked, that her own forehead was muddy. Since she didn’t know, that means my forehead is muddy.” So then both children know their foreheads are muddy, when the teacher asks a second time.
Now, this argument can be generalized to any (finite) number of children. The crucial concept here is common knowledge. We call a fact “common knowledge” if, not only does everyone know it, but everyone knows everyone knows it, and everyone knows everyone knows everyone knows it, and so on. It’s true that in the beginning, each child knew that all the other children had muddy foreheads, but it wasn’t common knowledge that even one of them had a muddy forehead. For example, if your forehead and mine are both muddy, then I know that at least one of us has a muddy forehead, and you know that too, but you don’t know that I know it (for what if your forehead were clean?), and I don’t know that you know it (for what if my forehead were clean?).
What the teacher’s announcement did, was to make it common knowledge that at least one child has a muddy forehead (since not only did everyone hear the announcement, but everyone witnessed everyone else hearing it, etc.). And once you understand that point, it’s easy to argue by induction: after the teacher asks and no child stands up (and everyone sees that no one stood up), it becomes common knowledge that at least two children have muddy foreheads (since if only one child had had a muddy forehead, that child would’ve known it and stood up). Next it becomes common knowledge that at least three children have muddy foreheads, and so on, until after a hundred rounds it’s common knowledge that everyone’s forehead is muddy, so everyone stands up.
The moral is that the mere act of saying something publicly can change the world—even if everything you said was already obvious to every last one of your listeners. For it’s possible that, until your announcement, not everyone knew that everyone knew the thing, or knew everyone knew everyone knew it, etc., and that could have prevented them from acting.
This idea turns out to have huge real-life consequences, to situations way beyond children with muddy foreheads. I mean, it also applies to children with dots on their foreheads, or “kick me” signs on their backs…
But seriously, let me give you an example I stole from Steven Pinker, from his wonderful book The Stuff of Thought. Two people of indeterminate gender—let’s not make any assumptions here—go on a date. Afterward, one of them says to the other: “Would you like to come up to my apartment to see my etchings?” The other says, “Sure, I’d love to see them.”
This is such a cliché that we might not even notice the deep paradox here. It’s like with life itself: people knew for thousands of years that every bird has the right kind of beak for its environment, but not until Darwin and Wallace could anyone articulate why (and only a few people before them even recognized there was a question there that called for a non-circular answer).
In our case, the puzzle is this: both people on the date know perfectly well that the reason they’re going up to the apartment has nothing to do with etchings. They probably even both know the other knows that. But if that’s the case, then why don’t they just blurt it out: “would you like to come up for some intercourse?” (Or “fluid transfer,” as the John Nash character put it in the Beautiful Mind movie?)
So here’s Pinker’s answer. Yes, both people know why they’re going to the apartment, but they also want to avoid their knowledge becoming common knowledge. They want plausible deniability. There are several possible reasons: to preserve the romantic fantasy of being “swept off one’s feet.” To provide a face-saving way to back out later, should one of them change their mind: since nothing was ever openly said, there’s no agreement to abrogate. In fact, even if only one of the people (say A) might care about such things, if the other person (say B) thinks there’s any chance A cares, B will also have an interest in avoiding common knowledge, for A’s sake.
Put differently, the issue is that, as soon as you say X out loud, the other person doesn’t merely learn X: they learn that you know X, that you know that they know that you know X, that you want them to know you know X, and an infinity of other things that might upset the delicate epistemic balance. Contrast that with the situation where X is left unstated: yeah, both people are pretty sure that “etchings” are just a pretext, and can even plausibly guess that the other person knows they’re pretty sure about it. But once you start getting to 3, 4, 5, levels of indirection—who knows? Maybe you do just want to show me some etchings.
Philosophers like to discuss Sherlock Holmes and Professor Moriarty meeting in a train station, and Moriarty declaring, “I knew you’d be here,” and Holmes replying, “well, I knew that you knew I’d be here,” and Moriarty saying, “I knew you knew I knew I’d be here,” etc. But real humans tend to be unable to reason reliably past three or four levels in the knowledge hierarchy. (Related to that, you might have heard of the game where everyone guesses a number between 0 and 100, and the winner is whoever’s number is the closest to 2/3 of the average of all the numbers. If this game is played by perfectly rational people, who know they’re all perfectly rational, and know they know, etc., then they must all guess 0—exercise for you to see why. Yet experiments show that, if you actually want to win this game against average people, you should guess about 20. People seem to start with 50 or so, iterate the operation of multiplying by 2/3 a few times, and then stop.)
Incidentally, do you know what I would’ve given for someone to have explained this stuff to me back in high school? I think that a large fraction of the infamous social difficulties that nerds have, is simply down to nerds spending so much time in domains (like math and science) where the point is to struggle with every last neuron to make everything common knowledge, to make all truths as clear and explicit as possible. Whereas in social contexts, very often you’re managing a delicate epistemic balance where you need certain things to be known, but not known to be known, and so forth—where you need to prevent common knowledge from arising, at least temporarily. “Normal” people have an intuitive feel for this; it doesn’t need to be explained to them. For nerds, by contrast, explaining it—in terms of the muddy children puzzle and so forth—might be exactly what’s needed. Once they’re told the rules of a game, nerds can try playing it too! They might even turn out to be good at it.
OK, now for a darker example of common knowledge in action. If you read accounts of Nazi Germany, or the USSR, or North Korea or other despotic regimes today, you can easily be overwhelmed by this sense of, “so why didn’t all the sane people just rise up and overthrow the totalitarian monsters? Surely there were more sane people than crazy, evil ones. And probably the sane people even knew, from experience, that many of their neighbors were sane—so why this cowardice?” Once again, it could be argued that common knowledge is the key. Even if everyone knows the emperor is naked; indeed, even if everyone knows everyone knows he’s naked, still, if it’s not common knowledge, then anyone who says the emperor’s naked is knowingly assuming a massive personal risk. That’s why, in the story, it took a child to shift the equilibrium. Likewise, even if you know that 90% of the populace will join your democratic revolt provided they themselves know 90% will join it, if you can’t make your revolt’s popularity common knowledge, everyone will be stuck second-guessing each other, worried that if they revolt they’ll be an easily-crushed minority. And because of that very worry, they’ll be correct!
(My favorite Soviet joke involves a man standing in the Moscow train station, handing out leaflets to everyone who passes by. Eventually, of course, the KGB arrests him—but they discover to their surprise that the leaflets are just blank pieces of paper. “What’s the meaning of this?” they demand. “What is there to write?” replies the man. “It’s so obvious!” Note that this is precisely a situation where the man is trying to make common knowledge something he assumes his “readers” already know.)
The kicker is that, to prevent something from becoming common knowledge, all you need to do is censor the common-knowledge-producing mechanisms: the press, the Internet, public meetings. This nicely explains why despots throughout history have been so obsessed with controlling the press, and also explains how it’s possible for 10% of a population to murder and enslave the other 90% (as has happened again and again in our species’ sorry history), even though the 90% could easily overwhelm the 10% by acting in concert. Finally, it explains why believers in the Enlightenment project tend to be such fanatical absolutists about free speech—why they refuse to “balance” it against cultural sensitivity or social harmony or any other value, as so many well-meaning people urge these days.
OK, but let me try to tell you something surprising about common knowledge. Here at SPARC, you’ve learned all about Bayes’ rule—how, if you like, you can treat “probabilities” as just made-up numbers in your head, which are required obey the probability calculus, and then there’s a very definite rule for how to update those numbers when you gain new information. And indeed, how an agent that wanders around constantly updating these numbers in its head, and taking whichever action maximizes its expected utility (as calculated using the numbers), is probably the leading modern conception of what it means to be “rational.”
Now imagine that you’ve got two agents, call them Alice and Bob, with common knowledge of each other’s honesty and rationality, and with the same prior probability distribution over some set of possible states of the world. But now imagine they go out and live their lives, and have totally different experiences that lead to their learning different things, and having different posterior distributions. But then they meet again, and they realize that their opinions about some topic (say, Hillary’s chances of winning the election) are common knowledge: they both know each other’s opinion, and they both know that they both know, and so on. Then a striking 1976 result called Aumann’s Theorem states that their opinions must be equal. Or, as it’s summarized: “rational agents with common priors can never agree to disagree about anything.”
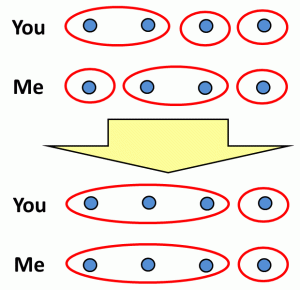
Actually, before going further, let’s prove Aumann’s Theorem—since it’s one of those things that sounds like a mistake when you first hear it, and then becomes a triviality once you see the 3-line proof. (Albeit, a “triviality” that won Aumann a Nobel in economics.) The key idea is that knowledge induces a partition on the set of possible states of the world. Huh? OK, imagine someone is either an old man, an old woman, a young man, or a young woman. You and I agree in giving each of these a 25% prior probability. Now imagine that you find out whether they’re a man or a woman, and I find out whether they’re young or old. This can be illustrated as follows:
The diagram tells us, for example, that if the ground truth is “old woman,” then your knowledge is described by the set {old woman, young woman}, while my knowledge is described by the set {old woman, old man}. And this different information leads us to different beliefs: for example, if someone asks for the probability that the person is a woman, you’ll say 100% but I’ll say 50%. OK, but what does it mean for information to be common knowledge? It means that I know that you know that I know that you know, and so on. Which means that, if you want to find out what’s common knowledge between us, you need to take the least common coarsening of our knowledge partitions. I.e., if the ground truth is some given world w, then what do I consider it possible that you consider it possible that I consider possible that … etc.? Iterate this growth process until it stops, by “zigzagging” between our knowledge partitions, and you get the set S of worlds such that, if we’re in world w, then what’s common knowledge between us is that the world belongs to S. Repeat for all w’s, and you get the least common coarsening of our partitions. In the above example, the least common coarsening is trivial, with all four worlds ending up in the same set S, but there are nontrivial examples as well:
Now, if Alice’s expectation of a random variable X is common knowledge between her and Bob, that means that everywhere in S, her expectation must be constant … and hence must equal whatever the expectation is, over all the worlds in S! Likewise, if Bob’s expectation is common knowledge with Alice, then everywhere in S, it must equal the expectation of X over S. But that means that Alice’s and Bob’s expectations are the same.
There are lots of related results. For example, rational agents with common priors, and common knowledge of each other’s rationality, should never engage in speculative trade (e.g., buying and selling stocks, assuming that they don’t need cash, they’re not earning a commission, etc.). Why? Basically because, if I try to sell you a stock for (say) $50, then you should reason that the very fact that I’m offering it means I must have information you don’t that it’s worth less than $50, so then you update accordingly and you don’t want it either.
Or here’s another one: suppose again that we’re Bayesians with common priors, and we’re having a conversation, where I tell you my opinion (say, of the probability Hillary will win the election). Not any of the reasons or evidence on which the opinion is based—just the opinion itself. Then you, being Bayesian, update your probabilities to account for what my opinion is. Then you tell me your opinion (which might have changed after learning mine), I update on that, I tell you my new opinion, then you tell me your new opinion, and so on. You might think this could go on forever! But, no, Geanakoplos and Polemarchakis observed that, as long as there are only finitely many possible states of the world in our shared prior, this process must converge after finitely many steps with you and me having the same opinion (and moreover, with it being common knowledge that we have that opinion). Why? Because as long as our opinions differ, your telling me your opinion or me telling you mine must induce a nontrivial refinement of one of our knowledge partitions, like so:
I.e., if you learn something new, then at least one of your knowledge sets must get split along the different possible values of the thing you learned. But since there are only finitely many underlying states, there can only be finitely many such splittings (note that, since Bayesians never forget anything, knowledge sets that are split will never again rejoin).
And something else: suppose your friend tells you a liberal opinion, then you take it into account, but reply with a more conservative opinion. The friend takes your opinion into account, and replies with a revised opinion. Question: is your friend’s new opinion likelier to be more liberal than yours, or more conservative?
Obviously, more liberal! Yes, maybe your friend now sees some of your points and vice versa, maybe you’ve now drawn a bit closer (ideally!), but you’re not going to suddenly switch sides because of one conversation.
Yet, if you and your friend are Bayesians with common priors, one can prove that that’s not what should happen at all. Indeed, your expectation of your own future opinion should equal your current opinion, and your expectation of your friend’s next opinion should also equal your current opinion—meaning that you shouldn’t be able to predict in which direction your opinion will change next, nor in which direction your friend will next disagree with you. Why not? Formally, because all these expectations are just different ways of calculating an expectation over the same set, namely your current knowledge set (i.e., the set of states of the world that you currently consider possible)! More intuitively, we could say: if you could predict that, all else equal, the next thing you heard would probably shift your opinion in a liberal direction, then as a Bayesian you should already shift your opinion in a liberal direction right now. (This is related to what’s called the “martingale property”: sure, a random variable X could evolve in many ways in the future, but the average of all those ways must be its current expectation E[X], by the very definition of E[X]…)
So, putting all these results together, we get a clear picture of what rational disagreements should look like: they should follow unbiased random walks, until sooner or later they terminate in common knowledge of complete agreement. We now face a bit of a puzzle, in that hardly any disagreements in the history of the world have ever looked like that. So what gives?
There are a few ways out:
(1) You could say that the “failed prediction” of Aumann’s Theorem is no surprise, since virtually all human beings are irrational cretins, or liars (or at least, it’s not common knowledge that they aren’t). Except for you, of course: you’re perfectly rational and honest. And if you ever met anyone else as rational and honest as you, maybe you and they could have an Aumannian conversation. But since such a person probably doesn’t exist, you’re totally justified to stand your ground, discount all opinions that differ from yours, etc. Notice that, even if you genuinely believed that was all there was to it, Aumann’s Theorem would still have an aspirational significance for you: you would still have to say this is the ideal that all rationalists should strive toward when they disagree. And that would already conflict with a lot of standard rationalist wisdom. For example, we all know that arguments from authority carry little weight: what should sway you is not the mere fact of some other person stating their opinion, but the actual arguments and evidence that they’re able to bring. Except that as we’ve seen, for Bayesians with common priors this isn’t true at all! Instead, merely hearing your friend’s opinion serves as a powerful summary of what your friend knows. And if you learn that your rational friend disagrees with you, then even without knowing why, you should take that as seriously as if you discovered a contradiction in your own thought processes. This is related to an even broader point: there’s a normative rule of rationality that you should judge ideas only on their merits—yet if you’re a Bayesian, of course you’re going to take into account where the ideas come from, and how many other people hold them! Likewise, if you’re a Bayesian police officer or a Bayesian airport screener or a Bayesian job interviewer, of course you’re going to profile people by their superficial characteristics, however unfair that might be to individuals—so all those studies proving that people evaluate the same resume differently if you change the name at the top are no great surprise. It seems to me that the tension between these two different views of rationality, the normative and the Bayesian, generates a lot of the most intractable debates of the modern world.
(2) Or—and this is an obvious one—you could reject the assumption of common priors. After all, isn’t a major selling point of Bayesianism supposed to be its subjective aspect, the fact that you pick “whichever prior feels right for you,” and are constrained only in how to update that prior? If Alice’s and Bob’s priors can be different, then all the reasoning I went through earlier collapses. So rejecting common priors might seem appealing. But there’s a paper by Tyler Cowen and Robin Hanson called “Are Disagreements Honest?”—one of the most worldview-destabilizing papers I’ve ever read—that calls that strategy into question. What it says, basically, is this: if you’re really a thoroughgoing Bayesian rationalist, then your prior ought to allow for the possibility that you are the other person. Or to put it another way: “you being born as you,” rather than as someone else, should be treated as just one more contingent fact that you observe and then conditionalize on! And likewise, the other person should condition on the observation that they’re them and not you. In this way, absolutely everything that makes you different from someone else can be understood as “differing information,” so we’re right back to the situation covered by Aumann’s Theorem. Imagine, if you like, that we all started out behind some Rawlsian veil of ignorance, as pure reasoning minds that had yet to be assigned specific bodies. In that original state, there was nothing to differentiate any of us from any other—anything that did would just be information to condition on—so we all should’ve had the same prior. That might sound fanciful, but in some sense all it’s saying is: what licenses you to privilege an observation just because it’s your eyes that made it, or a thought just because it happened to occur in your head? Like, if you’re objectively smarter or more observant than everyone else around you, fine, but to whatever extent you agree that you aren’t, your opinion gets no special epistemic protection just because it’s yours.
(3) If you’re uncomfortable with this tendency of Bayesian reasoning to refuse to be confined anywhere, to want to expand to cosmic or metaphysical scope (“I need to condition on having been born as me and not someone else”)—well then, you could reject the entire framework of Bayesianism, as your notion of rationality. Lest I be cast out from this camp as a heretic, I hasten to say: I include this option only for the sake of completeness!
(4) When I first learned about this stuff 12 years ago, it seemed obvious to me that a lot of it could be dismissed as irrelevant to the real world for reasons of complexity. I.e., sure, it might apply to ideal reasoners with unlimited time and computational power, but as soon as you impose realistic constraints, this whole Aumannian house of cards should collapse. As an example, if Alice and Bob have common priors, then sure they’ll agree about everything if they effectively share all their information with each other! But in practice, we don’t have time to “mind-meld,” swapping our entire life experiences with anyone we meet. So one could conjecture that agreement, in general, requires a lot of communication. So then I sat down and tried to prove that as a theorem. And you know what I found? That my intuition here wasn’t even close to correct!
In more detail, I proved the following theorem. Suppose Alice and Bob are Bayesians with shared priors, and suppose they’re arguing about (say) the probability of some future event—or more generally, about any random variable X bounded in [0,1]. So, they have a conversation where Alice first announces her expectation of X, then Bob announces his new expectation, and so on. The theorem says that Alice’s and Bob’s estimates of X will necessarily agree to within ±ε, with probability at least 1-δ over their shared prior, after they’ve exchanged only O(1/(δε2)) messages. Note that this bound is completely independent of how much knowledge they have; it depends only on the accuracy with which they want to agree! Furthermore, the same bound holds even if Alice and Bob only send a few discrete bits about their real-valued expectations with each message, rather than the expectations themselves.
The proof involves the idea that Alice and Bob’s estimates of X, call them XA and XB respectively, follow “unbiased random walks” (or more formally, are martingales). Very roughly, if |XA-XB|≥ε with high probability over Alice and Bob’s shared prior, then that fact implies that the next message has a high probability (again, over the shared prior) of causing either XA or XB to jump up or down by about ε. But XA and XB, being estimates of X, are bounded between 0 and 1. So a random walk with a step size of ε can only continue for about 1/ε2 steps before it hits one of the “absorbing barriers.”
The way to formalize this is to look at the variances, Var[XA] and Var[XB], with respect to the shared prior. Because Alice and Bob’s partitions keep getting refined, the variances are monotonically non-decreasing. They start out 0 and can never exceed 1 (in fact they can never exceed 1/4, but let’s not worry about constants). Now, the key lemma is that, if Pr[|XA-XB|≥ε]≥δ, then Var[XB] must increase by at least δε2 if Alice sends XA to Bob, and Var[XA] must increase by at least δε2 if Bob sends XB to Alice. You can see my paper for the proof, or just work it out for yourself. At any rate, the lemma implies that, after O(1/(δε2)) rounds of communication, there must be at least a temporary break in the disagreement; there must be some round where Alice and Bob approximately agree with high probability.
There are lots of other results in my paper, including an upper bound on the number of calls that Alice and Bob need to make to a “sampling oracle” to carry out this sort of protocol approximately, assuming they’re not perfect Bayesians but agents with bounded computational power. But let me step back and address the broader question: what should we make of all this? How should we live with the gargantuan chasm between the prediction of Bayesian rationality for how we should disagree, and the actual facts of how we do disagree?
We could simply declare that human beings are not well-modeled as Bayesians with common priors—that we’ve failed in giving a descriptive account of human behavior—and leave it at that. OK, but that would still leave the question: does this stuff have normative value? Should it affect how we behave, if we want to consider ourselves honest and rational? I would argue, possibly yes.
Yes, you should constantly ask yourself the question: “would I still be defending this opinion, if I had been born as someone else?” (Though you might say this insight predates Aumann by quite a bit, going back at least to Spinoza.)
Yes, if someone you respect as honest and rational disagrees with you, you should take it as seriously as if the disagreement were between two different aspects of yourself.
Finally, yes, we can try to judge epistemic communities by how closely they approach the Aumannian ideal. In math and science, in my experience, it’s common to see two people furiously arguing with each other at a blackboard. Come back five minutes later, and they’re arguing even more furiously, but now their positions have switched. As we’ve seen, that’s precisely what the math says a rational conversation should look like. In social and political discussions, though, usually the very best you’ll see is that two people start out diametrically opposed, but eventually one of them says “fine, I’ll grant you this,” and the other says “fine, I’ll grant you that.” We might say, that’s certainly better than the common alternative, of the two people walking away even more polarized than before! Yet the math tells us that even the first case—even the two people gradually getting closer in their views—is nothing at all like a rational exchange, which would involve the two participants repeatedly leapfrogging each other, completely changing their opinion about the question under discussion (and then changing back, and back again) every time they learned something new. The first case, you might say, is more like haggling—more like “I’ll grant you that X is true if you grant me that Y is true”—than like our ideal friendly mathematicians arguing at the blackboard, whose acceptance of new truths is never slow or grudging, never conditional on the other person first agreeing with them about something else.
Armed with this understanding, we could try to rank fields by how hard it is to have an Aumannian conversation in them. At the bottom—the easiest!—is math (or, let’s say, chess, or debugging a program, or fact-heavy fields like lexicography or geography). Crucially, here I only mean the parts of these subjects with agreed-on rules and definite answers: once the conversation turns to whose theorems are deeper, or whose fault the bug was, things can get arbitrarily non-Aumannian. Then there’s the type of science that involves messy correlational studies (I just mean, talking about what’s a risk factor for what, not the political implications). Then there’s politics and aesthetics, with the most radioactive topics like Israel/Palestine higher up. And then, at the very peak, there’s gender and social justice debates, where everyone brings their formative experiences along, and absolutely no one is a disinterested truth-seeker, and possibly no Aumannian conversation has ever been had in the history of the world.
I would urge that even at the very top, it’s still incumbent on all of us to try to make the Aumannian move, of “what would I think about this issue if I were someone else and not me? If I were a man, a woman, black, white, gay, straight, a nerd, a jock? How much of my thinking about this represents pure Spinozist reason, which could be ported to any rational mind, and how much of it would get lost in translation?”
Anyway, I’m sure some people would argue that, in the end, the whole framework of Bayesian agents, common priors, common knowledge, etc. can be chucked from this discussion like so much scaffolding, and the moral lessons I want to draw boil down to trite advice (“try to see the other person’s point of view”) that you all knew already. Then again, even if you all knew all this, maybe you didn’t know that you all knew it! So I hope you gained some new information from this talk in any case. Thanks.
Update: Coincidentally, there’s a moving NYT piece by Oliver Sacks, which (among other things) recounts his experiences with his cousin, the Aumann of Aumann’s theorem.
Another Update: If I ever did attempt an Aumannian conversation with someone, the other Scott A. would be a candidate! Here he is in 2011 making several of the same points I did above, using the same examples (I thank him for pointing me to his post).


 Follow
Follow
Comment #1 August 16th, 2015 at 5:05 pm
I recently did a YouTube video on a version of the Muddy Children Puzzle:
Comment #2 August 16th, 2015 at 5:29 pm
Wow! great stuff here… I just wish Lewis Carroll was alive to read it! (…but then you probably knew that I could guess that you would know that I would wish that).
Comment #3 August 16th, 2015 at 6:37 pm
Really cool! I attended the first SPARC, where I got exposed to Aumann’s Theorem but didn’t get any more context on it; this post really clarified everything. Guess I should have gone back to visit this year!
Comment #4 August 16th, 2015 at 6:42 pm
I don’t know if this is useful to anyone, but here’s how I reasoned backwards to convince myself that “At least one child has a muddy forehead” was not common knowledge prior to the teacher’s saying it.
Because I don’t know if my own forehead is muddy, I can only confidently assert that 99 foreheads are muddy. Now say I pick another child to compare my knowledge against. I know that the two of us can confidently agree that the other 98 children have muddy foreheads, but since neither of us know about our own foreheads, we can’t do any better than that. Now say I compare my knowledge and the second child’s to a third child’s. The three of us can only confidently agree about the other 97 children, and so on.
In general, n children only have common knowledge about the foreheads of the other 100-n children. But then if we look at the group as a whole, there is no forehead that everyone can agree is muddy, and so there is no common knowledge.
Comment #5 August 16th, 2015 at 6:45 pm
A liberal opinion is composed of several sub opinions so you can so can expect that you will gain a more liberal opinion without knowing which of the subopinoins will be the one that changes
Comment #6 August 16th, 2015 at 6:53 pm
(Hi Scott! I’ve been reading this blog for a while, but I’ve never felt compelled to comment until now.)
“rational agents with common priors can never agree to disagree about anything.”
I think this summary is a case of imperfectly mapping a theoretical result to human language. For me at least, agreeing to disagree can also mean you agree on a meta level that it is not a good idea to attempt to resolve your concrete disagreement right now, e.g. two people agree they have better things to do than to discuss the expectation of random variable X, since there are variables Y and Z that are much more useful/interesting. One should be careful before turning formal results into slogans that are easy to misunderstand.
The above example leads us to the interesting question of how to even choose which variable X we should be updating at all. It seems to me there is already a significant complexity barrier there. How would you encode a discussion e.g. on the israel/palestine debate in terms of these random variables? How can you make sure that when you are talking about X, your discussion partner is not thinking of X’, a related but different concept that happens to be described by the same human words? How do you recall facts from your fallible human brain without also dredging up involuntary emotional reactions and associations to other topics? How do you estimate the utility of a certain action when neither you nor anyone else ca ever know the state of mind of any person other than maybe yourself?
As a separate issue, it seems to me that our brains do not store facts separately, but rather by heavily associating and diffing on top of previously established thoughts. My brain at least is definitely not unbounded and I certainly don’t have perfect recall. Modeling it as an infinitely large slab of RAM is therefore a bit suspect.
Please forgive me if I sound a bit confrontational; it is precisely because I am fascinated by the possible applicability of this type of thing that I ask these hard questions. For the time being, I will stick to my intuitive opinion that this kind of rationality can never be achieved by human beings (or computers for that matter) due to severe complexity limitations, even though I don’t have a theorem that proves it (yet?).
Comment #7 August 16th, 2015 at 8:55 pm
So you suggest that a true Bayesian will disregard the rationality or correctness of any argument because all that matters (in the true Bayesian sense) is that some information about the other person is now known, i.e. the updating of information is more important than the content of that information. But doesn’t that assume that the other person is speaking truthfully and honestly? If the first person intentionally lies, then this doesn’t seem to work, i.e. they won’t converge.
Or, more to the point, aren’t each of the people (in a perfectly Bayesian argument) inherently assuming that both of them are Bayesian? What if one isn’t but the other doesn’t know he/she isn’t?
Clearly, fact-laden fields make it easy to pick out someone who is lying since “facts” in such fields are independently verifiable. But when you get into the muddled world of politics or gender issues or something like that, things get murkier. For instance, suppose I’m a politician and I avidly oppose gay marriage in a debate. But maybe I’m just doing that to be politically expedient (in fact a lot of politicians seem to be like this). This is the very definition of flip-flopping in politics — say whatever it is that you think your audience wants to hear.
In short, what happens when only one party in the argument is truly Bayesian but the Bayesian one assumes they both are?
(Incidentally, I completely agree with the moral of the story — try to see things from other people’s perspective.)
Comment #8 August 16th, 2015 at 8:56 pm
#1 is not all surprising if you follow psychology and especially behavioral genetics. There’s increasingly a lot of evidence linking political and moral and philosophical attitudes to deeper cognitive attitudes (not just Haidt’s work), and all of these are highly heritable. Given strong predispositions like these, it obviously breaks the requirements for Aumannian agreement: not only is there no reason to expect our priors to be common, there’s no reason for us to be updating the same way!
eg in no particular order, some relevant papers: “Genetic Influences on Political Ideologies: Genome-Wide Findings on Three Populations, and a Mega-Twin Analysis of 19 Measures of Political Ideologies from Five Western Democracies”, “Genetic Influence on Human Psychological Traits: A Survey”, Bouchard 2004 https://pdf.k0nsl.org/krystallnacht.com/Science/Genetics%20E-books/Genetic%20Influence%20on%20Human%20Psychological%20Traits%3B%20A%20Survey%20by%20Thomas%20J.%20Bouchard.pdf ; “Are Political Orientations Genetically Transmitted?”, Alford et al 2005 http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1006&context=poliscifacpub ; “The Importance of Heritability in Psychological Research: The Case of Attitudes”, Tesser 1993 http://www2.psych.ubc.ca/~schaller/528Readings/Tesser1993.pdf (some tables of the ubiquity of heritability: https://i.imgur.com/0PcO2Bf.png https://i.imgur.com/RSNUWS2.png ); “Not by Twins Alone: Using the Extended Family Design to Investigate Genetic Influence on Political Beliefs”, Hatemi et al 2010 http://www.matthewckeller.com/16.Hatemi.et.al.2010.Nuc.fam.ajps.pdf http://www.pnas.org/content/83/12/4364.short ; “Differences in negativity bias underlie variations in political ideology”, Hibbing et al 2014 https://pdf.yt/d/KsatVxjZ_2CROOhc https://www.dropbox.com/s/q6l9ixeq5g66a0i/2014-hibbing.pdf http://www.motherjones.com/politics/2014/07/biology-ideology-john-hibbing-negativity-bias http://experimentalphilosophy.typepad.com/experimental_philosophy/2012/07/personality-predicts-professional-philosophers-beliefs.html
Comment #9 August 16th, 2015 at 9:19 pm
In the first part where you were talking about common knowledge. Sociologists have already named this. It’s just a specific case of Thomas’ theorem.
https://en.wikipedia.org/wiki/Thomas_theorem. And social psychologists from a cognitive background study this sort of thing everyday. In most cases, it’s not the objective facts that matter but how people perceive these facts that led them to act in certain ways. So common knowledge doesn’t become common unless people already know that other people already know about this and that they also know that everyone else.
Comment #10 August 16th, 2015 at 9:23 pm
Vitor #6: Our two Bayesian agents could, of course, decide not to carry out the Geanokoplos-Polemarchakis protocol right now, or to do it but for a different question. But if, by that protocol or by any other means, their opinions about question X become common knowledge, then at that point their opinions about question X must be equal. So, it’s in that sense that people in the field (following Aumann) say they can’t “agree to disagree”: they can’t have common knowledge of differing opinions. I agree that the terminology is a little imprecise, since it elides the common knowledge requirement.
Comment #11 August 16th, 2015 at 9:27 pm
Robin Hanson is famous for saying politics is not about policy or X isn’t about the aumanian ideal of X it is really about status and power and alliances. There major differences between arguments, negotiations, performances, and games.
If you call out people for not performing the Auman ideal, aren’t you doing the equivalent of saying “lets go exchange fluid?”
If the argument is really about who would win a fight, then you might be more likely to start them if you call out Aumanian failure.
-Alex-
Comment #12 August 16th, 2015 at 9:31 pm
Ian #7: Yes, absolutely, common knowledge of rationality and honesty is one of the background assumptions here—one that was referred to in the post but should have been brought out more explicitly. IIRC, there’s some literature on variants of Aumann’s Theorem where you relax that assumption (anyone else want to provide references? if not I’ll try to later). But the simplest interpretation is, again, that these results have aspirational significance: they describe what conversations should look like between two people whose honesty and rationality are so ironclad that neither one doubts the other doubts it, nor doubts the other one doubts they doubt it, etc.
Comment #13 August 16th, 2015 at 9:19 pm
Nick #4: Yes, thanks for that, and sorry for the omission!
I love the image of the mud disappearing from the foreheads one by one, as child 1 contemplates what it’s possible to child 2 that it’s possible to child 3 that…
Comment #14 August 16th, 2015 at 10:43 pm
AlexJ #12: In this post, I didn’t “call out” anyone for “not performing the Aumannian ideal”—I’m perfectly well aware of the mite in one’s own eye there, etc. I did suggest that, inspired by the “Aumannian ideal,” all of us make more of an effort to think about how persuasive our arguments would be to us had we been born into different circumstances.
Also, even if I had called someone out for Aumannian shortcomings, I fail to understand how that would be like crudely requesting sex from them. But maybe that just goes to show my nerdiness and social naivete all the more!
Comment #15 August 17th, 2015 at 1:31 am
I assume you met a bunch of other wannabe rational people in Berkeley, and you had shared opinions with them and such. Were your (non-mathematical) discussions more like Aumannizing or more like bargaining? An example or two would be great!
Comment #16 August 17th, 2015 at 2:52 am
James Miller, nice video. Thanks.
Comment #17 August 17th, 2015 at 4:40 am
>> the easiest!—is math
So how does the Grundlagenstreit, the fight between Hilbert and Brouwer, fit into this?
Another question is why evolution did not move us (yet) further towards those rational information exchanges – what is the advantage of not being Bayesian? There must be good reason people behave irrationally.
Could one prove that if everybody is an honest Bayesian then the one person which is not gains an advantage?
Comment #18 August 17th, 2015 at 5:24 am
Hi! I am a bit puzzled that dont’ you spend more time talking about the formal properties of “common belief”. A while ago people noticed that our ability to agree to disagree might simply mean that Aumann’s and al. formalization of “knowledge” does not reflect the ordinary content of that concept
http://www.tau.ac.il/~samet/papers/ignoring.pdf
Comment #19 August 17th, 2015 at 5:51 am
Wolfgang #17, You should be careful in assigning evolution an intentionality that is just not there.
I think that this situation is just an instance of the price of anarchy. Evolution works on individuals, making them converge towards a Nash equilibrium, not the social optimum. It would require a simultaneous change in a large proportion of the population to break out of such an equilibrium.
As long as we are in a society where most people lie, play status games, defend their tribal affiliations, etc, being 100% honest and rational tends to hurt us as individuals.
Comment #20 August 17th, 2015 at 7:07 am
@Vitor #17
>> intentionality
I don’t , but if Bayesianism is the best way to acquire information about the world (which should increase survival rates), then why are we, and I include our animal colleagues here, not all rational Bayesian updaters?
The fact is that without proper training we are not even able to calculate probabilities very well.
Comment #21 August 17th, 2015 at 7:39 am
“Muddy Foreheads” When explaining the inductive process you use the phrase:
(since if only had child had had a muddy forehead, that child would’ve known it and stood up)
I think should be:
(since if only ONE had child had had a muddy forehead, that child would’ve known it and stood up)
Comment #22 August 17th, 2015 at 7:48 am
Great post!
Some real-world effects that might be interesting to try to incorporate into the model:
1. differing prior beliefs about each other’s honesty or rationality
2. some sort of hierarchical model where the beliefs that can be communicated depend strongly on hidden “background assumption” variables that the actors disagree on and that cannot be communicated directly
3. the “filter bubble” scenario: what kinds of “trust priors” lead a population to bifurcate into two groups that cannot reconcile their beliefs?
Comment #23 August 17th, 2015 at 8:14 am
Zach #21: Thanks, fixed!
Comment #24 August 17th, 2015 at 8:25 am
wolfgang #17: As I mentioned in the OP, my comments about math only apply to situations where all the participants at least agree about the ground rules—not to philosophical debates like formalism versus intuitionism.
There are many, many reasons why evolution could have produced “irrational” minds, ranging from simple computational limitations, to the value of irrationality as a commitment device (“if you wrong me, I WILL get revenge”), to (possibly) the need for self-deception when building a modular mind. These are all active topics of cognitive science research; you could try Steven Pinker’s books (again) for a nice introduction.
Comment #25 August 17th, 2015 at 8:33 am
Shmi #15: As I said, outside of well-defined parts of math and science, my own conversations are almost never “Aumannian” (are anyone’s??). Then again, most of my conversations aren’t exactly non-Aumannian either: they’re simply not about trying to reach the truth about an empirical question where the parties disagree. Some of them are straightforward sharing of information known to one party but not the other, others are for amusement, etc.
I did talk to some SPARC folks about the many-worlds interpretation, the hard problem of consciousness, and I forget what else (they were choosing the topics). Of course, these sorts of things are tricky to fit into the Aumannian framework, since even if all the empirical facts (about which it makes sense to have a “prior”) were fixed, people might still disagree about them. I recall the conversations as extremely respectful and friendly, albeit not particularly Aumannian.
Comment #26 August 17th, 2015 at 8:39 am
@Scott #24
>> many, many reasons
I agree, but I think you left out an important one: Bayesianism and, in general, calculating probabilities, does not work very well in the real world.
Let’s take your simple example of guessing 2/3 of the average number:
The stupid answer would be a random positive number.
The smarter one would be 0.
But then we have to estimate the probability that not all people iterate the problem to the end and if we assume this probability is non-zero we have to use a number away from zero. So are we now back to being stupid or really smart?
And once we know that some “really smart” people will guess above zero, what is the probability distribution then? etc. etc.
And is it rational to spend so much effort just to come up with some number in game, what is the probability that some people conclude they rather not spend too much time on it? etc. etc.
And this was a simple example.
Comment #27 August 17th, 2015 at 8:57 am
@Wolfgang #20
I think bayesianism is very effective at the society level, but not at the individual level. That is, a society full of bayesian reasoners seems like it would have an advantage over other societies, but a bayesian individual tends to have a disadvantage against their peers in a predominantly non-bayesian society. Efficient Knowledge aquisition doesn’t protect you very well from other members of your society turning against you, and there are few others with whom to engange in Aumannian knowledge swaps. The ability to interact with others (be that to successfully cooperate in group activities or knowing how to get a leg up on your rivals) is a lot more important in a survival focused society than being more efficient at any particular task as an individual.
Let me illustrate with an example: When lions are competing against zebras, they will evolve to be faster, have sharper claws, etc. However, when lions dominate their environment, they will evolve to kill their rivals’ cubs. In this case inter- and intra-species fitness optimization produce vastly different results.
Comment #28 August 17th, 2015 at 9:50 am
Very nice post! Here are a few remarks: First, I wrote an essay about Aumann: Science, beliefs and knowledge: a personal reflection on Robert J. Aumann’s approach. Which mention some of Aumann’s work and a specific long disagreement between the two of us. As a matter of fact, in spite of Aumann’s theorem we hardly agree, and we often agree to disagree. Once we discovered that on a certain political matter we agree! We were so surprised to find that we shared the same opinion, that we decided to write a “letter to the editor” containing our position on the matter. When we got to the fine details, “agreeing to agree” was impossible.
Second, two reason (among several) for why Aumann’s theorem and related insights fails in reality is the difficulty to assign probabilities to events, and sensitivity to noise. This applies to very simple application of Bayesian pronciples and certainly to recursive repeated applications, e.g., if we need to reach detailed priors (also based on our proprs based on the possibility that I am another person etc.) Indeed some economics, based on such Bayesian and Aumannian insights advocate a change in the judicial system that will allow jurors to receive and weigh all information, including prior criminal records of the defendant, the track records of the lawyers, the opinion of the press, etc. They argue that a Bayesian process based on all available information will yield optimal results. One can be skeptical about this advice and argue that the “noise sensitivity” of a complicated Bayesian process will make the outcomes meaningless.
Third, kudos for Scott for the non macabre presentation of the puzzle. On the other hand, Pinker’s made-up story is fairly offensive and can teach us, perhaps, on how date-rapes come about. “Yes, both people know why they’re going to the apartment, but they also want to avoid their knowledge becoming common knowledge. ” Reality is not like that, and certainly it is often not like that. Even if etching is not it, people often don’t have the clear picture in mind (and certainly often not the same picture in mind) on why they’re going to the apartment.
Last, Scott wrote: “I would urge that even at the very top, it’s still incumbent on all of us to try to make the Aumannian move, of “what would I think about this issue if I were someone else and not me?”
I fully and enthusiastically support this statement. Even if not to influence your own thinking it is often damn interesting to figure out how other people think about things.
Comment #29 August 17th, 2015 at 9:59 am
Does the last bit of Scott’s post mean that the “Veil of Ignorance” approach used to judge a moral position can, in some sense, be derived from Aumann’s Theorem?
Comment #30 August 17th, 2015 at 10:58 am
Bringing it down to the case of three children, all with muddy foreheads:
Every child knows that at least one forehead is muddy (because they see at least one muddy forehead), and that everyone knows that at least one forehead is muddy (because, for everyone else in the room, everybody sees at least one muddy forehead that person sees.
What they don’t know is that everyone knows that everyone knows that at least one forehead is muddy; in order to do that, they would need to see that, for every child a, for every other child b, child a saw a muddy forehead that child b also saw.
With 100 students, the chain of “know-knows” is 100 or so long, and it comes to “Child dx isn’t sure that child dw is sure that… child a knows that someone has mud on their face.”
Comment #31 August 17th, 2015 at 11:10 am
In your hierarchy of fields, I might put philosophy at the very top. I feel like some social justice arguments actually do get resolved, with rational argument playing some role.
Also, isn’t the part of geography with Aumannian arguments a pretty small part of the field these days?
Comment #32 August 17th, 2015 at 11:44 am
My guess (strictly amateur) is that non-Aumannian disagreements standout because they are interesting. These are presumably vastly outnumbered by points on which any two bayesian agents (or real people for that matter) will agree on and more or less take for granted (e.g. probability that the sun will rise tomorrow).
As a commenter noted upstream, these comparatively rare points of disagreement are interesting and important because they underlie status and power relationships. In science, careers are based on winning arguments by publishing a better posterior hypothesis than the next guy at each round of the “negotiation”. When and if agreement is eventually reached, whose contribution was greater?
As much as conservative economists claim to love efficient markets that reach agreement on fair prices, real businesses do everything in their power to avoid them – at least for their particular product. Market power is key to profit. Making a profit from an efficiently priced commodity takes a lot more work. Hence, intellectual property laws are designed to limit the reach of markets by creating artificial monopolies, etc.
A thermodynamic analogy. Given time, a chemical reaction will reach equilibrium. However, equilibrium is usually a boring place to be because there is no available free energy. Free energy being a measure of how far a reaction is from equilibrium.
So if we didn’t have non-Aumannian disagreements we’d have to invent them (and so maybe we did ;).
Comment #33 August 17th, 2015 at 11:49 am
This is excellent, thank you for sharing. I can’t figure out what’s going on in your graphical example of a nontrivial knowledge partition. So the dots represent possible states of the world, the red circles represent sets of states that the agent can differentiate between (“I don’t know who the culprit is, but I know which red circle they’re a member of “), and then the two agents share info and both wind up at the state of knowledge on the bottom. But by my understanding, perfect knowledge would be represented by having every dot in its own circle, and that would mean that the agents shared information and both got dumber somehow. Could you clarify this?
Comment #34 August 17th, 2015 at 12:02 pm
Thinking about it some more, i got it backwards. It’s more like “I don’t know who the culprit is, but I would if you told me which red circle they’re a member of”. So if I can differentiate between A and B, and you can differentiate between B and C, then together we can differentiate between A, B, and C. Duh.
Comment #35 August 17th, 2015 at 12:59 pm
Scott—
Is there a technical introduction to shared-knowledge that you’d recommend to a total beginner in that area? I found this post interesting but when it got to the discussion of Aumann’s theory I got a little lost. Hoping to learn, just looking for a good entry.
Cheers,
Joey
Comment #36 August 17th, 2015 at 1:12 pm
Joey #35: I think my own paper is fairly accessible! (Until it gets to all the various improvements and generalizations of the 1/(δε2)) result, but those are also the parts that a beginner can skip.)
The Cowen and Hanson paper is more accessible, though also not very technical.
Aumann’s original 1976 paper (which is like 3 pages), and the later papers by Geanakoplos et al. and others, are also quite clear (except that they’re often concerned with the generalization to infinite state spaces, or other issues that I don’t especially care about).
Finally, the book and survey “Reasoning About Knowledge” provide a nice introduction to muddy-children puzzles, common knowledge, etc., although they don’t go much into Aumann theory.
Comment #37 August 17th, 2015 at 1:16 pm
[…] Archive Show HN: Kalu – Calculator concept for long and inter-linked calculations Futures of text Common Knowledge and Aumann’s Agreement Theorem Alienable Rights (1992) A Scripting Language for HTTP Self-Reliance by Ralph Waldo Emerson (1841) […]
Comment #38 August 17th, 2015 at 1:34 pm
I might not be so quick to sing the praise of academic disagreements as Aumannian.
In my experience in physics, the opinion-switching thing definitely happens. But I think we’re still far away from the Aumannian ideal.
Scientists tend to be better at incorporating the other person’s arguments and updating on those, which causes the side-switching on the blackboard. But I don’t think we’re any better at updating purely from the fact that the other person disagrees. In fact we might be worse — whenever someone says something I disagree with, I say “why do you think that?” and then do my update on their explanation. I don’t think anyone ever changes their beliefs before the other person has even explained, which is what an Aumannian ideal would do.
Which is just to say that maybe scientists are one step closer (updating on the other person’s justifications, at least), but still a long ways away from actually updating just based on the other person’s beliefs.
Comment #39 August 17th, 2015 at 1:46 pm
Scott #36: Your “survey” link currently points back to this page, I’m guessing this is not what you intended?
Comment #40 August 17th, 2015 at 2:05 pm
I don’t think these puzzles properly take into account rational willingness to take a guess and later correct the error if the guess is wrong. If one is a child who can see 99 children with muddy foreheads, then even deprived of the ability to communicate apparent novelties (for example, to point out Billy’s lack of mud on his forehead), there still *ought* to be some inferrable probability that one’s own forehead is muddy. (Possibly 99/100?)
So, a “rational” human in that situation would not engage in a complex series of increasingly ludicrous thoughtloops. A rational human would simply assume that it is rather unlikely that oneself is a dramatic exception to a perceived norm, and take the bet that one’s own forehead is muddy.
If one turned out to be wrong about one’s unexceptionality, one can generally update that information, unless the error is fatal. And if it is known that the error may be fatal, one is generally advised to look about for the mud-puddle, and smear one’s forehead (and the forehead of loved ones) whether it originally had mud on it or not
Social enforcement is fundamentally a problem simplification mechanism, perhaps?
Comment #41 August 17th, 2015 at 2:15 pm
And if social enforcement is primarily a problem-simplification tool, then this explains why stupider and/or less patient people are more likely to engage in it, because they want problems to be simple. Hence the intellectual adversity of conservatism, and conformism of any kind – *what* the principle one is forced to conform *to* is irrelevant, so long as it is basically simple. Binary gender, racial heirarchy, table manners, religious practices, etc. Intellectually-oriented people appear to be less likely to conform on one or more social norms than the average, although not necessarily across *multiple* social norms. Enforcers are happy to use stimulus-response aversion therapies, after all – the mechanisms are simple.
Comment #42 August 17th, 2015 at 2:36 pm
Gil #28:
Pinker’s made-up story is fairly offensive and can teach us, perhaps, on how date-rapes come about.
Speaking of other people’s perspectives, did you ever consider the possibility that the above statement might offend me? Date-rapes don’t just “come about”; they’re committed by perpetrators who make a deliberate decision to press on despite their victims’ wishes. Pinker was writing, instead, about the reality of social ambiguity—a reality that many people navigate effortlessly, though it can make life hell for nerds and people on the autism spectrum. (Or to use the language to which I was so graciously exposed over the last year: helloooo? neurotypical privilege, anyone? 😉 )
I saw nothing offensive about the story: if Steven Pinker is a bigot, then may I strive every day to be 1% the bigot that he is! Even so, given my past experience (!#@!), before retelling the story, I carefully and deliberately cleansed it of any literary flourishes that I feared might conceivably offend someone. If you still call the result “offensive,” then aren’t you essentially saying that there’s no possible way to discuss the actual substantive question I wanted to discuss—namely, whether difficulty dealing with “knowledge that’s not common knowledge” is an important contributor to nerds’ social miseries—in any way you’d find acceptable? Do you ever worry that people who get that message will eventually say, “OK then, to hell with inoffensive, inclusive language, if it fails anyhow at its goal, which is to get people to focus on the ideas themselves rather than their feeling of being offended by their airing”?
Comment #43 August 17th, 2015 at 2:47 pm
Sniffnoy #39: Thanks, fixed!
Comment #44 August 17th, 2015 at 3:45 pm
Hi Scott, I addressed the criticism to Pinker and not to you and tried to be as positive as I could to your judgments and choices and ideas in the other parts of the comment. So I did try not to offend you and I am sorry if I did offend you. (I did criticize people in the past for telling the main puzzle story in a macabre or sexist way and I am happy you found a better way.) I don’t think and didn’t say that Pinker is a bigot. All I know about him is from this post and this single puzzle.
The example is problematic. (maybe Pinker was careful about his wording and maybe it was written in times when people were less aware about it.) It would be interesting to read what he actually wrote.
Let’s go over Pinker’s puzzle: Your date tells you: would you like to come up for a coffee and you say yes sure. the puzzle is this: both you and your date know perfectly well that the reason they’re going up to the apartment has nothing to do with coffee but rather to have sex. They probably even both know the other knows that. But, then why don’t they just blurt it out: “would you like to come up for some intercourse?”
The answer according to Pinker (as you described it) is common knowledge. Pinker was writing about the reality of social ambiguity—a reality that many people navigate effortlessly, though it can make life hell for nerds and people on the autism spectrum.
But Scott, the reality is that this is not the reality. In most cases of such a scenario the issue is not common knowledge, the issue is that of simple knowledge. Even if both partners know that they want something beyond coffee it may be a different thing. There are perhaps some cases that they both want sex and know it, but not common know it. But there are other cases where one wrongly assumes that the invitation for coffee means an invitation for sex, and Pinker’s reality puzzle is negative in this respect. I am sure that there are better ways to talk about social ambiguity and common knowledge, just like you found a better way to describe the main puzzle without killing anybody.
Comment #45 August 17th, 2015 at 3:58 pm
Decius #30
>What they don’t know is that everyone knows that everyone knows that at least one forehead is muddy; in order to do that, they would need to see that, for every child a, for every other child b, child a saw a muddy forehead that child b also saw.
But isn’t it the case that they both can see child C who has a muddy forehead? While I understand why between 2 children there’s no common knowledge, I can’t explicitely formulate an equivalent statement that would work for a group of 3.
Comment #46 August 17th, 2015 at 3:59 pm
I knew a lady who worked at a VLSI fab equipment manufacturer, programming the electron-beam lithography machines. These were the machines that made the masks that the chip wafers were printed with. The masks were pieces of glass covered with photoresist-like material that you’d expose with the e-beam and then dissolve away the unexposed parts with acid, sort of like making a printed circuit board, except you could write much finer details, down to micron size in those days (nanometers now). She had made some test masks with very beautiful patterns and kept them in her apartment. So she used to joke that when she invited people up to see her etchings, she really meant it ;-).
Comment #47 August 17th, 2015 at 6:12 pm
thank you, that was fascinating.
I went and read Gil’s recollections of Aumann, and Oliver Sacks, and Steven Pinker on etchings..
In high school and for some years after, I expected people to be rational. That turns out to be irrational.
Aumann’s argument falls at the first hurdle, ‘two rational agents’ – where is there even one to be found ?
“If you can find but one person who deals honestly and seeks the truth, I will forgive this city.” Jeremiah 5:1
Comment #48 August 17th, 2015 at 7:24 pm
asdf #46: LOL, that’s an awesome story!
Yeah, contrary to Gil’s reading, I think it’s clear from the post that, as long as there’s not common knowledge (as created by an explicit statement), but only probable knowledge about probable knowledge about probable knowledge, etc., with the degree of certainty decreasing with each iteration, either party can super-easily terminate at any time. That is, either one gets to say: “thank you, these are beautiful etchings! OK, I should be going now…” Or: “glad you liked my etchings! Should I call you a cab home?” Furthermore, the fact that either party reserves the ability to do that, without even the minor “loss of face” of going back on a common-knowledge agreement, is part of the entire point of these cliched circumlocutions (as I mentioned in the post), making Gil’s objection particularly ironic and strange. Yes, you can argue that we’d all be better off if everyone were completely explicit and direct about what they wanted—that would be an interesting argument to make—but to suggest that a common-knowledge account of the “etchings paradox” implicitly condones date-rape seems utterly wrong to me.
[Addendum: Rape would, of course, still be rape even if one of the parties had said, “would you like to come up for some intercourse?” but then changed their mind once they got upstairs. For that reason, the question of how direct or indirect the parties are when outside the building seems completely orthogonal to the question of consent.]
Incidentally, if you want to get an idea of what Pinker said, you can do Amazon Look Inside on Pinker’s book and search for “etchings.”
Comment #49 August 17th, 2015 at 7:32 pm
Incidentally, I should mention that my paper proves the 1/(δε2) theorem by looking at the expectations of XA2 and XB2. Yan Zhang, an instructor at SPARC, suggested to me that it might be more intuitive to talk about Var[XA] and Var[XB] (which, in this case, are off from the expected squares by an unchanging constant), and I decided to adopt his nice suggestion in the blog post—for one thing, because the latter looked better when rendered in HTML. 🙂
Comment #50 August 17th, 2015 at 8:32 pm
It’s also worth noting that if things go badly, good chance both parties are going to want to deny their original intentions. For this reason, you don’t even need full plausible deniability, but only the potential for the two of you to plausibly deny it together! I don’t know if that’s related to levels of common knowledge, though.
Comment #51 August 17th, 2015 at 10:00 pm
Martin-2 #33, #34: The red ovals represent the states of the world that the agent in question can’t currently distinguish from each other. Thus, it makes perfect sense that as the agents learn more, the ovals get smaller and more numerous (with the limit being a separate red circle around each state). Conversely, when the agents reason about what the other considers it possible that the other considers it possible that … etc., the ovals grow larger, taking in more and more possible states.
Comment #52 August 17th, 2015 at 10:15 pm
D #31:
In your hierarchy of fields, I might put philosophy at the very top. I feel like some social justice arguments actually do get resolved, with rational argument playing some role.
That sounds more wondrous than a unicorn! 😀 Can you point me to an example?
I’ve participated in many debates about AI, consciousness, the interpretation of quantum mechanics, mathematical Platonism, etc. with people from all walks of life, that resulted in the participants saying they now understood each others’ views better, they’d never considered that position before, etc. Whereas from my observations, social-justice arguments always seem to end with ad hominems, vilification campaigns (if not threats and doxxing), and both sides feeling angrier and more aggrieved than before—or, as the “best” outcome, with one side bullied and cowed into submission, publicly recanting and apologizing for causing offense even while silently muttering that its arguments went unanswered. This is why, back in December, I did that little experiment to see whether it might be possible to get past that dynamic, with mixed results…
Also, isn’t the part of geography with Aumannian arguments a pretty small part of the field these days?
I confess that I don’t really know what geographers do these days. Maybe you or someone else could explain it?
Comment #53 August 17th, 2015 at 11:49 pm
The common knowledge part of what “Would you like to come up to my apartment for a cup of coffee?” has become so common that if you did indeed want to invite your date up for a cup of coffee and nothing more you’d hesitate because it becomes so difficult to convey that what’s considered common knowledge isn’t applicable in a specific case.
Comment #54 August 18th, 2015 at 12:02 am
Hi Scott. On why we don’t observe Aumannian conversation in the real world (comments 13 and 7 and probably more I missed):
1. On topics such as politics we don’t trust our opponents, so honesty and rationality do not hold. But even on topics such as maths where honesty and rationality do hold, after 1 round of messages a disagreement conversation typically progresses to something else entirely: information transfer. it’s not enough that I know your opinion; I want to know how you arrived there. Along the way I will play the sceptic to force you to give me the information I crave.
In other words, the “disagreement” part of the discussion is very short and looks much more Aumannian than the rest of the discussion.
2. I can’t recall a single disagreement in maths or any other topic in which the parties have completely switched sides. I suppose I could imagine it happening along Aumannian lines, but I’m surprised to hear you say that it’s a “common” occurrence.
Why don’t we see more switching? I’d guess it has something to do with not having an accurate enough model of what’s going on in the other party’s head, or perhaps failing to allow what you do know of the other party to influence your own opinion. Irrationality, in other words. 🙂
Comment #55 August 18th, 2015 at 12:06 am
An interesting piece !
I was wondering about the scenario if the common knowledge assumed by – “since not only did everyone hear the announcement, but everyone witnessed everyone else hearing it, etc.” – is untrue, e.g., if a few muddy children could not hear the announcement. How will the argument proceed in that case ?
Comment #56 August 18th, 2015 at 12:30 am
Nice piece. A question though. Do you think the kids got the point you were driving at?
Comment #57 August 18th, 2015 at 1:19 am
Sorry Scott, I was not aware of of the “Etchings” euphemism while reading Pinker’s story.
Comment #58 August 18th, 2015 at 2:13 am
The situation in the other Scott A’s post (regarding everyone hating Stalin but no one knowing that) is something like pluralistic ignorance:
https://en.wikipedia.org/wiki/Pluralistic_ignorance
I think I might have learned that concept here on this blog some time back.
Comment #59 August 18th, 2015 at 3:18 am
aviti #56: Not only did they get it, they already knew a large fraction of what was in the talk. These were extremely smart kids.
Comment #60 August 18th, 2015 at 3:21 am
Gus #54:
I can’t recall a single disagreement in maths or any other topic in which the parties have completely switched sides. I suppose I could imagine it happening along Aumannian lines, but I’m surprised to hear you say that it’s a “common” occurrence.
Really? I’m thinking of cases where A is trying to prove some conjecture, while B thinks there’s a counterexample … but then, after seeing why some attempted counterexamples fail, B changes her mind and thinks the conjecture holds. So then A switches to playing devil’s-advocate and starts looking for counterexamples, etc.
Comment #61 August 18th, 2015 at 3:26 am
Rahul #53:
The common knowledge part of what “Would you like to come up to my apartment for a cup of coffee?” has become so common that if you did indeed want to invite your date up for a cup of coffee and nothing more you’d hesitate because it becomes so difficult to convey that what’s considered common knowledge isn’t applicable in a specific case.
That’s an amusing observation, but notice that you switched from the technical meaning of “common knowledge” to the colloquial meaning—which, in this case, means almost the opposite! I.e., you’re saying that it’s common knowledge in the colloquial sense, that inviting your date up for coffee is a way to avoid making your intentions common knowledge in the technical sense. 🙂
Comment #62 August 18th, 2015 at 5:16 am
Dear Scott, can you (or anyone here) give a reference to the actual study of the 2/3 guessing game that you mentioned?
Comment #63 August 18th, 2015 at 5:39 am
Oleg #62: Try the references at https://en.wikipedia.org/wiki/Guess_2/3_of_the_average.
Comment #64 August 18th, 2015 at 7:41 am
Scott #46 and others: I think a rational person (at least a heterosexual rational person of childbearing age) should *always* make their intentions explicit in the “etchings” case. That’s because after the question “Would you like to see my etchings, and then some sex if you are still interested?”, if the answer is positive, the next question should be “What kind of birth control do you prefer?”
This has huge benefits to the rationalist. First, the answer to the birth control question could result in enormous state updates (compare “None, I’m hoping to get pregnant” to “I’m sterile, unfortunately”). Second the rationalist may realize they may not behave as rationally in other circumstances (ie. in the abstract, they would not have sex if there was a 5% chance of someone getting pregnant, but after a few drinks and in the middle of hot and heavy petting, they might agree to sex with that odds of a mishap). This is similar to a rationalist who enjoys gambling but still would not take a big wad of cash to the casino. Finally (and maybe this is a geek rationalist thing) it just feels better to know that you tried to minimize the odds of future regret, for both parties.
Comment #65 August 18th, 2015 at 8:24 am
The Quakers (and their ancestral Anabapists and Mennonites) have a highly successful 350-year tradition of staunchly supporting social justice objectives, while staunchly rejecting vilification, threats, and anger.
Recommendation Scott, were you (and other Shtetl Optimized readers) to attend a Friendly meeting for unprogrammed worship — meetings that are always wholly open and welcoming to the general public — you might attain to an experience-grounded appreciation of how a young Baruch Spinoza, having been vilified, threatened, and doxxed by his own community, found a crucial shelter for his young mind, spirit and body within these long-standing and thorough-goingly Aumannian communities.
Observation At any given Friends meeting, a substantial portion of the community commonly are independent-minded practicing therapists, very much in the tradition of young Scott Alexander (and young Spinoza too), who arrive from every religious tradition and none.
Proposition For the fostering of Aumannian cognition, the personal experience of a single Friendly unprogrammed meeting can be more enlightening than any amount of interweb wrangling.
Comment #66 August 18th, 2015 at 8:29 am
Rationality and honesty are assumed, but I’m not clear how incorrect information/observation fits into this.
Should each agent also apply a probability for the data to be wrong? (like my instrument could fail 5% of the time)
Comment #67 August 18th, 2015 at 9:48 am
Scott #61:
Indeed! My blunder. I didn’t even realize it till you pointed it out!
PS. Science should stop borrowing colloquial terms and assigning them totally counterintuitive technical meanings. 🙂
e.g. Take the statistical usage of the term “significant”. Turns out that many things statistically significant are often non-significant in the practical sense of the word. These two definitions of significance are almost orthogonal. So much confusion has been caused by this tricky usage.
Maybe Aumann ought to have named this “recursively transparent knowledge” or something! 🙂
Comment #68 August 18th, 2015 at 10:12 am
@wolfgang #17 re why we are not bayesian
That’s because the complexity of the inference on a bayesian network is O(exp(n)), and we mere P creatures can only aspire to an approximation thereof! Thus “bounded rationality” as it’s called in the literature (what Scott alluded to by people stopping after some levels of indirection instead of reasoning to infinity).
Comment #69 August 18th, 2015 at 11:48 am
[…] 2. Common knowledge and Aumann’s agreement theorem. […]
Comment #70 August 18th, 2015 at 11:57 am
A couple months ago, TED-Ed made an animation describing a version of the Muddy Children Puzzle (with green-eyed children, and no one dying):
Comment #71 August 18th, 2015 at 12:41 pm
I know some Bayesian statisticians, and I’d consider myself a Bayesian thinker, but I’ve never heard of this selling point. On the contrary, most Bayesians seem to think that the good part is that Bayesianism gives you a meaningful and rigorous way to update your subjective probabilities, and the fact that you have to have a subjective prior in the first place is a major inconvenience.
You seem have some observations I don’t; could you elaborate?
Comment #72 August 18th, 2015 at 12:44 pm
@AI hobbyist #68
OK, but my point is/was that n is very large in real world examples, so even an approximation by us “mere P creatures” is usually not very informative.
Somebody mentioned above the probability p that the sun will not rise tomorrow. Well, we probably all agree that p is very small, but this is not much better than what people estimated e.g. in the Middle Ages.
If one wants to actually calculate p, the question of how many small black holes are near our solar system would be needed as input; a quantity not known very well.
How about a gamma ray burst that would wipe us out and how about some other more exotic possibilities?
And how about the scenario that we are just a computer simulation and somebody turns it off “tomorrow” – what prior would we assign to that case? etc. etc.
Perhaps one could get an estimate from the many times the sun was rising already without fail, but what is the probability that this history is “fake”?
Where does a real Bayesian draw the line outside of textbook examples which tell him what possibilities to consider?
In other words, in the real world I would not know how to even get started on a real bayesian calculation of p, because n is (quasi)infinite.
Comment #73 August 18th, 2015 at 12:52 pm
“Would you like to see my etchings, and then some sex if you are still interested?”
Well, I thought I would, and of course I don’t give a damn about etchings. But as a rationalist myself I must update my priors. If you need to sort this question out explictly, then chances are you’re not especially paying attention to me as a person. That’s not necessarly bad -truth is, I was looking for casual sex. But ask for yourself: is it reasonable to think, conditioned on you’re not willing to play the seduction game, that you’ll be a decent lover? By the way, at least we can now reach an Aumann’s agreement about our favorite method for birth control together: abstinence. 🙂
Comment #74 August 18th, 2015 at 1:17 pm
Re #68
Isn’t that the idea Scott proved wrong in the present post?
Comment #75 August 18th, 2015 at 6:47 pm
I’m in agreement with Janne #71. The way it’s written (a selling point) sounds like Bayesians value having a subjective prior that they know is vastly different from somebody else’s (and still feel right about their own conclusion).
The appeal of Bayesianism that it recognizes that you cannot avoid subjective priors, which could be your own, or the only prior in the world available to everybody.
Comment #76 August 18th, 2015 at 7:02 pm
Marylin #73: In the scenario you amusingly describe, that doesn’t sound at all like an Aumannian agreement, but—to whatever extent there any factual questions at issue—more like agreeing to disagree. 🙂
Comment #77 August 18th, 2015 at 7:08 pm
Janne #71 and Koray #75: OK, given that there’s not really any question of fact at issue, I’ll happily grant to my Bayesian friends that subjectivity is a weakness rather than a selling point of their approach. 🙂 I was thinking, for example, of Chris Fuchs, who often sings the praises of Bayesian subjectivity in the context of his QBist (Quantum Bayesian) approach to quantum mechanics. But maybe a better way to put it would be: Bayesians consider it a selling point of their approach that it’s explicit about the unavoidability of subjective starting beliefs (as encoded in the prior), rather than trying to sweep that under the rug.
Comment #78 August 18th, 2015 at 8:03 pm
Sort of relevant, all this talk of rationality reminded me of this gem from writings of Seth Lloyd:
“Ironically, it is customary to assign our own predictable behavior and that of other humans to rationality: we’re we to behave rationally, we reason, the world would be more predictable. In fact, it is just when we behave rationally, moving logically, like a computer, from step to step, that our behavior becomes provably unpredictable. Rationality combines with self-reference to make our actions intrinsically paradoxical and uncertain.”
Comment #79 August 18th, 2015 at 11:01 pm
Nick #78: That statement seems to require some pretty big asterisks…
(1) Some computations are trivial to predict.
(2) “Behaving rationally” is not at all the same thing as “behaving like a computer.” A computer can make arbitrarily “irrational” decisions if you program it to.
(3) Sure, there exist mathematically well-defined problems (e.g., predicting the long-time behavior of another program) that provably take a long time to solve, but that doesn’t mean mathematically ill-defined problems are easier to solve! 🙂
Comment #80 August 19th, 2015 at 3:39 am
Thanks Scott, I suddenly don’t understand it again! The bottom graphs represent the agents modeling each other? Ah I see, it says so right there in the words. This makes more sense now.
Comment #81 August 19th, 2015 at 12:52 pm
Nice read! Scott, is any of this inspired by the short exchange we had regarding courage and homophobia?
Comment #82 August 19th, 2015 at 6:10 pm
Don’t the things we disagree about generally derive from differences of values (utility functions) rather than expectations (priors)?
From there, disagreement over expectations can arise because of hidden priors, hidden motivations, deception (and meta-deception) in service of conflicting values. For example, if a child wanted to short-circuit this stupid game, he could just stand up in round 98.
I could just be completely wrong, point me to the part of the article that would explain why.
Comment #83 August 19th, 2015 at 10:34 pm
Jona #81: I’ve been interested in Aumann’s theorem since I learned about it in 2003. But while I wasn’t motivated by any single exchange (and I don’t even remember the one you mention), I can say that my interest in the questions of how to get rational people to see each other’s perspectives, and how fundamental disagreements between them can indefinitely persist, were certainly stimulated further by my recent blog experiences.
Comment #84 August 19th, 2015 at 10:41 pm
leibniz #82: If differences in moral values lead people to different factual beliefs (i.e., expectations over future experiences), then yes, dishonesty or irrationality (or self-deception, or call it whatever you like) are probably in play—since presumably we agree that the world is what it is, with how it ought to be having no causal power over its state. So yes, as the post said, one might be able to account for Aumann’s theorem’s failure to describe real people on that ground alone. But as the post also said, in that case Aumann’s theorem would still have aspirational significance: it would still describe what our disagreements ought to look like, if we fancy ourselves honest and rational.
Comment #85 August 20th, 2015 at 10:22 am
Scott #83: Sorry, I was a bit naive about the amount of discussion you do here 🙂
What I meant was; here you said,
“even if you know that 90% of the populace will join your democratic revolt provided they themselves know 90% will join it, if you can’t make your revolt’s popularity common knowledge, everyone will be stuck second-guessing each other, worried that if they revolt they’ll be an easily-crushed minority. And because of that very worry, they’ll be correct!”
And a while back you said, “it’s more valuable to speak a moral truth that no one in your social circle recognizes than one that everyone in your circle recognize”, and with this later part I disagreed, basically pointing out how sometimes, it could be more important to establish common ground and consensus. Even called you “phallocentric” over it.
Comment #86 August 20th, 2015 at 11:25 am
How robust is the Muddy Children puzzle to uncertainty? Suppose that it is common knowledge that every child assigns probability 0.5 to having mud on her face, believe the teacher’s statement to be truthful with probability \(0.5 + \epsilon\), and will stand up once her probability of having mud on her faces exceeds \( 1 – \delta \). When if ever do the children stand up?
Comment #87 August 20th, 2015 at 12:46 pm
Hi Scott,
A few months ago you had a very interesting post about Eigenmorality and a Prisoner Dilemma software competition under Eigenjesus and Eigenmoses criteria.
I think it would be interesting to have another run of Prisoner Dilemma competition under the Common Knowledge scenario. That is, make source code of all participating programs available to all other programs so that they could make decision not only on the previous history but also on the analysis of the opponent’s algorithm. That could be an interesting AI challenge: analyze a program that analyzes you analyzing it. 🙂
Comment #88 August 20th, 2015 at 4:13 pm
Hi Scott-
I think there are some other options for escaping Aumann’s theorem that I didn’t see on a quick read of your post above: (1) Deny that the intuitive notion of “public information” (ie common knowledge) actually corresponds to the technical notion of common knowledge. (2) Allow that people sometimes update on false propositions. (3) Allow that people aren’t perfectly introspective – sometimes they know things but don’t know that they know them.
I go through the details of how (2) and (3) allow escape from Aumann’s theorem in a paper that recently came out in the Review of Symbolic Logic. [In my own view (1) is also very important, but it’s obvious how that would work formally. Actually I’m inclined to think we don’t have common knowledge in the technical sense.] The paper’s here:
http://users.ox.ac.uk/~hert2388/People%20with%20Common%20Priors%20Can%20Agree%20to%20Disagree.pdf
The math is elementary, and you can cut through the introductory stuff to the pictures representing the models, Unfortunately these additional ways of resisting the result don’t seem to have been sufficiently well-recognized.
(I also show that you only need to relax the assumption that it’s common knowledge that any of the relevant assumptions hold. Once you see this, I don’t think Aumann’s result even puts that much pressure on a very strong form of Bayesianism, as I say in the paper.)
Harvey
Comment #89 August 20th, 2015 at 5:02 pm
[…] https://scottaaronson-production.mystagingwebsite.com/?p=2410 […]
Comment #90 August 20th, 2015 at 7:13 pm
Michael P #87: Some people at MIRI actually ran such a tournament; they called it “Modal Kombat.” You can read the paper here.
Comment #91 August 21st, 2015 at 3:54 pm
“Instead, merely hearing your friend’s opinion serves as a powerful summary of everything your friend knows that could possibly be relevant to the question.”
I do not believe this is true (have you updated towards it not being true yet? No? Fine, I’ll give you the argument while grumbling about Aumann.) In particular, there’s no guarantee that the Aumannian probability reached after having common knowledge of each others’ rational credence’s, equals the probability reached after sharing all information known.
To give a simple example: our shared prior over the bias of a coin is:50% it is fair, 50% it only lands on heads. We go our separate ways, and each happen to see a single flip of the coin. It is heads for both of us. Our posteriors are both 2/3 in the heads one, and as much as we have common knowledge of the others’ posterior, this will not change. (it’s possible that we each saw the same flip.) *
However, were we to share all our evidence, we’d now have a shared posterior of 4/5 (because we’d compare dates and see that the flips were different, so we have twice as much evidence).
Am I doing something wrong? I hesitate to accuse you of a mistake, you’re the math expert here, but the claim seems indefensible to me.
* Actually, you should be updating based on the chance that the evidence is new, but I haven’t worked that out fully yet and didn’t want to complicate the post. Your claim would still be wrong, because the info that it wasn’t the same flip isn’t included in the probability, but say you think there’s a 50% chance that their evidence is not the same as yours, you should do a “half-update” towards including that evidence.
Second: “Like, if you’re objectively smarter or more observant than everyone else around you, fine, but to whatever extent you agree that you aren’t, your opinion gets no special epistemic protection just because it’s yours.”
In practice, many of the opinions you reject *are* because you think you’re smarter/more rational/better informed/less biased than the person you’re arguing with.
Comment #92 August 21st, 2015 at 5:52 pm
This is a very interesting post from my point of view. I didn’t know about Aumann’s theorem before.
It seems to me, however, that most opinions that people may agree to disagree about are more aptly characterised as (fairly complex) algorithms to interpret or act upon information about the world than as different numerical values for something simple like the expected value of a single random variable. In the opinions-as-programs setting, then, it does seem very hard to me for agents bounded in terms of communications bandwidth and/or computational capacity to truly arrive at “common knowledge” in the required technical sense or to perform the required bayesian adjustments.
To elaborate, suppose I’m a truth-seeking, honest, rational chess computer with sufficient additional intelligence to engage in dialogue with fellow chess computers about the evaluation of chess positions. In this case, it is conceivable that by way of Aumannian dialogue about a position that myself and another computer strongly disagree about, I may reach a consensus opinion about the value of that particular position with fairly limited communications and calculation; but it will be very hard for me to change in a meaningful way my approach to judging the next chess position we may encounter, because my current approach will already be a carefully-tuned locally optimal solution to the problem of playing chess well with the computational resources I’m given and even if another program managed to send me their full source code, it would be a highly nontrivial problem to use that information to improve my own algorithms. Thus, the outcome of that Aumannian conversation would seem to inevitably be:
1. Both parties agree that for some particular positions which were under discussion, the evaluation algorithm used by the other side has merits; maybe their pawn structure evaluation was not that far off, in that example.
2. Both parties by and large stay with the locally optimal approaches to chess playing that they have already found, because improving on either of the two algorithms is genuinely hard given their computational resources.
3. Possibly, both sides learn from their conversation to predict with high accuracy how the other side would play in any given situation (i.e. they gain common knowledge). However, this doesn’t help them in practice because using that knowledge productively would require essentially doubling their own computational capacity in order to run both algorithms in parallel, which they cannot do.
In that second sense, the two sides would then “agree to continue disagreeing”. They would both know that after any amount of conversation that they may engage in, and notwithstanding any agreement that they may reach about the value of a thousand individual positions, there will still be billions of other legal chess positions that both programs will strongly disagree about.
This does not appear to be in contradiction to experience with regards to conversations about e.g. politics.
After all, most opinions that people disagree about would correspond to much more involved computational procedures than the two different chess playing algorithms in the fictitious example above.
Am I missing something obvious or is this a way out of the apparent contradiction between the Aumannian theorem and the reality of conversations between supposedly relatively rational, honest agents that was not discussed in the post?
As a final thought, it is also worth noting that there are indeed conversations where humans will behave (for better or worse) as is expected for Aumannian rational agents. For instance, many people will believe the result of computer calculation with much less sanity checks than would be advisable given the possibilities of e.g. numerical error or algorithm incorrectness.
Comment #93 August 21st, 2015 at 9:44 pm
I see a big problem with minds that start behind Rawls’ “veil of ignorance” trying to use Bayesian inference. The only prior that such minds can have in common is to expect a totally chaotic universe, in which the probabilities of all events are mutually independent. And just looking at Bayes’ equation shows that, in such a universe, every piece of new evidence yields the trivial update: the posterior probability of every event is exactly equal to the prior probability. For a mind behind Rawls’ veil, Bayesian inference is logically valid but practically useless.
As a result, Cowan and Hanson’s argument that all of us really have the same prior collapses. My initial judgements that two events are related can’t have come from Bayesian methods. Therefore I can’t assume that anyone of whom I know nothing makes the same judgements that I do. So, even assuming rationality and honesty in all parties, different priors are the expected norm, and Aumann’s theorem doesn’t generally apply.
Comment #94 August 21st, 2015 at 10:16 pm
I’m flying to South Korea today, and might not have time to answer all the interesting objections here! But:
Michael #93: Your argument only works if you assume the minds would have a uniform prior over all possible sequences of perceptions. But, just like even newborns are extremely far from blank slates, it seems to me that even a pure Spinozist reasoner need not have a uniform prior. Many of the people who think about these things talk instead about the “universal prior,” where you weight every possible sequence of perceptions by 2 to the minus its Kolmogorov complexity. (Or if you like: you assume your experience is the output of a random self-delimiting computer program.) Crucially, you can prove that the specific choice of programming language changes the probabilities by at most a constant–so while it biases you, in the limit of a large number of observations that bias goes away. You could think of the universal prior as a formal implementation of the idea that Occam’s Razor is a primitive rule of reasoning: something any rational mind simply has to assume from the outset, since trying to derive it from experience inevitably leads to circularity.
There are plenty of arguments one could level against the universal prior; I set out some of them myself in an appendix to The Ghost in the Quantum Turing Machine. But at any rate, this is a much more sophisticated idea than a uniform prior over experiences, and not as obviously wrong.
Comment #95 August 21st, 2015 at 10:38 pm
Avi #91: You’re absolutely right, and I’ll amend that sentence in my post. Thank you.
When I wrote, “merely hearing your friend’s opinion serves as a powerful summary of everything your friend knows that could possibly be relevant to the question,” I was trying to convey an intuition for how Aumann’s Theorem could possibly hold. But while there’s something true in the vicinity of that sentence, the sentence itself is false, as you correctly point out.
Here’s a simpler counterexample than yours: let the bits x and y be uniformly random, and suppose Alice knows only x while Bob knows only y. They then hold a conversation about the probability that x=y. Of course, even before they’ve exchanged a word, they completely agree about that probability: it’s 50%! And no matter how many times they reassure each other that their probabilities are still 50%, neither will learn anything new and the probabilities won’t budge. And yet, if they exchanged “everything they knew that could possibly be relevant to the question” (namely, x and y themselves), they would learn the ground truth, and their probabilities would become either both 0% or both 100%.
I’d love to claim this as a case where I, being a virtuous rationalist, changed my mind in response to what you said. But embarrassingly, if you read my paper, you’ll find a detailed exploration of the exact point above! I.e., that the goal of an agreement protocol is just to make Alice and Bob agree with each other, and that the answer they converge on might be arbitrarily far from the “ground truth” that they would know if they exchanged their inputs.
So, this is a case where you and I already agreed, but then rhetorical excess led me to write something at odds with the correct understanding that we agreed about, and your pointing it out brought me back to the True Path. I wonder how many real-life comings-to-agreement have that structure?
Comment #96 August 21st, 2015 at 10:54 pm
Incidentally, Avi #91:
In practice, many of the opinions you reject *are* because you think you’re smarter/more rational/better informed/less biased than the person you’re arguing with.
Yes, of course. Two obvious responses:
1. If you notice that almost everyone considers themselves to be smarter, more rational, and less biased than most of the people around them (not to mention a better driver etc.), and then reflect that most people must be wrong in their self-assessments, that should probably cause you to be way less confident about whether you can use such beliefs to discount other people’s opinions in your own case. (On the other hand, there’s also the classic paradox: that the people most in need of this sort of advice are probably the least likely to heed it, while the people who genuinely wrestle with such humbling self-reflections, and who therefore trust themselves least, probably do have objective grounds for trusting their own judgments more than their neighbors’.)
2. There are cases where someone says something like: “Alice is obviously brilliant and honest, and knows way more about this subject than I do, but she and I just agree to disagree about this particular question.” It seems to me that understanding Aumann’s theorem should at least prompt careful reflection about those cases in your own life.
Comment #97 August 22nd, 2015 at 12:28 am
I appreciate Zhang’s advice about how you should present this paper. I read through the paper about a week ago and did not at all understand its math because the notation was very dense. But this blog post, by talking about how the variance is essentially a martingale, made it very easy to understand.
Comment #98 August 23rd, 2015 at 1:30 pm
If we were objectively rational mutual knowledge would be based on the factually verifiable so disagreement would not be possible
Comment #99 August 23rd, 2015 at 2:14 pm
I’d like to reinforce #82.
Moral value is not the only kind of value, and in particular there is also epistemic value. Different styles of epistemology put different weightings on empirical evidence, as opposed to theoretical argument, authority, and so on. Atheists don’t think the Bible is evidence, climate change sceptics don’t think models are evidence.,etc, etc. Aumanns theorem is regularly criticised for oversimiplification, and one of the less commonly mentioned simplifications is that both parties agree on what “information” is… in realistic situations, that is a very complex question.
Comment #100 August 23rd, 2015 at 2:25 pm
“…almost everyone considers themselves to be smarter,”
There is a funny story about Aumann himself regarding it. In one heated department meeting, the chairman at the time Lior, said, “Some people in this department think that they are smarter than they really are, ” Aumann immediately replied, “I am actually smarter than I think I am.”
Comment #101 August 23rd, 2015 at 10:46 pm
This is great, I’ve heard Aumann’s Theorem a couple of times but never understood it.
I think I like it even less now that I think I understand it, though ;-). I don’t even accept it as a good aspiration. Consider this except from Mercier and Sperber’s “Why do humans reason?” explaining circumstances under which confirmation bias could actually be helpful in seeking the truth ( http://www.dan.sperber.fr/wp-content/uploads/2009/10/MercierSperberWhydohumansreason.pdf )
In this view, disagreements, even the kinds of disagreements that lead to apparent irrationalities like confirmation bias and motivated reasoning can still be socially useful because they motivate us to take a diverse set of approaches to a problem. (Thus, in order to rationally disagree from the group, it isn’t necessary to believe that you are smarter or more rational than everybody else, only that your personal viewpoint is one worth exploring.)
That’s not to say that mathematicians and scientists are wrong to be switching blackboard sides when they feel the urge. But other fields aren’t necessarily wrong to maintain their disagreements–because disagreements and diversity of opinions are useful cognitive resources that shouldn’t be given up all in one go.
Comment #102 August 24th, 2015 at 12:29 pm
Humans have very fallible memories. For that reason, we tend to argue with beliefs rather than actual facts. Along our life’s journey, we gather facts that weight our beliefs. Many of these facts are probably forgotten. Once there’s a deeply established belief it takes a sledge hammer of a fact(s) to dislodge it. I would say that applies to even the most reasonable/logical of us all.
Comment #103 August 24th, 2015 at 11:15 pm
This makes me thing of Daniel Patrick Moynihan’s terrific quote, “Everyone is entitled to his own opinions, but not his own facts.”
Comment #104 August 26th, 2015 at 1:11 pm
I think it is worth to mention another point. Perhaps Aumann’s Theorem does not hold in “real life”, because his model is finite, however the world is infinite. This is loosely related to the complexity issue mentioned in the post (point (4)). In an infinite model it can happen that it is not an event that an event is commonly known, so the players do not know that the event is commonly known. Of course the players know the event, but they do not know that the event is commonly known. In this framework Aumann’s Theorem does not hold.
I think if one looks at the credit rating companies she can see that those agree to disagree!
Comment #105 August 28th, 2015 at 1:05 pm
Pete#103:
Which is a cute saying and all are impressed you can remember it, so if that was your goal, props.
As you’re undoubtedly aware it doesn’t actually apply here, because I wasn’t talking about incorrect facts, rather correct ones both remembered and possibly forgotten, nevertheless understood to be correct.
I also just happened to read an article that talked about MRI imagining of the brain while arguing which showed flight or fight centers activating rather than logic centers. An interesting observation worth noting.
Comment #106 August 30th, 2015 at 11:46 pm
Fascinating–this post/discussion seems to be emanating from some kind of alternate universe inhabited by beings remarkably like humans, except that they are motivated primarily by a dispassionate search for objective truth. I’d be very interested in meeting such creatures one day. I know that there are those–particularly in academia–who speculate about the possibility of such organisms existing, but given everything I know about evolutionary pressures, it’s hard for me to see how organisms whose thought processes worked that way–as opposed to concentrating on self-serving goals–could ever manage to evolve…
Comment #107 August 31st, 2015 at 6:27 am
I’d like to join Gil Kalai in commending your beautiful exposition of Aumann’s agreement theorem. However, I beg to differ with both of you on its normative value in certain areas.
Clearly, one easy way out of the theory vs. practice dilemma that you pose is to do away with the supposition that the purpose of a debate is to improve the parties understanding of the world. As you explain so neatly, making something common knowledge has a real influence on the actions of the agents involved, and most practical debates are conducted where the agents have some utility over the pursuing actions. Clearly, in such cases it would be useless to appeal to the normative value of an Aumannian debate.
So the more interesting question concerns the normative value in academic debates. An easy way out of the dilemma would be to claim that some academic fields aim not to learn more about the objective reality, but to shape a social or political reality, so the previous argument applies. So what we’re really asking is whether or not debates that aim to study the world should be Aumannian. In Math, the answer is clearly yes. I am not so sure the same answer applies, for instance, to social sciences. The reason is the following. When we do research in math, we do so under the assumption that we have the tools to resolve completely for eternity the problem we’re researching. As we move away from the fragment of math that is effectively decidable, this assumption fades. It is largely true in exact sciences, but it is perfectly reasonable to assume that in social sciences we are very far away from possessing the information to resolve questions definitively. In such a case there is likely to be an innate benefit to keep controversy alive, rather than to converge to common knowledge. The reason is that our search for evidence, as Popper and Hayek and others noted, is not independent of our state of knowledge. So if you want to widen the search in hope for better results in the long run, you want different researchers to have different states of knowledge. This is a bit like the role of genetic diversity in evolution.
Comment #108 August 31st, 2015 at 1:27 pm
Would you like to come up for a coffee?
I don’t drink coffee.
That’s OK. I haven’t got any.
Comment #109 August 31st, 2015 at 5:26 pm
Cool post. Pretty sure the highshchoolers got out with stars in their eyes.
Comment #110 September 21st, 2015 at 9:09 pm
[…] and whether rational people can agree to disagree. It covers a lot of the same ground as my recent post on the same topic, except with less technical detail about agreement theory and more … […]
Comment #111 October 7th, 2015 at 10:04 pm
As you note, it isn’t always the case that people can think through the various levels. Here’s a “real-life” example.
Scene from “Seinfeld” The Phone Message (TV Episode 1991):
(Donna and George are in George’s car, outside her apartment, after dinner together.)
Donna: So, er, thanks for dinner. It was great.
George: Yeah. We should do this again.
Donna: Would you like to come upstairs for some coffee?
George: Oh, no, thanks. I can’t drink coffee late at night, it keeps me up.
Donna: (Looks disappointed) So, um, OK.
George: OK.
Donna: Goodnight.
George: Yeah, take it easy.
(Donna leaves car. George realizes what he has done and bashes his forehead in disgust)
Comment #112 October 30th, 2015 at 12:43 pm
Sorry if this has been covered in the comments above since I didn’t read all of them. My question is that it is implicit in Aumann’s theorem that the information function of each agent is partitional. Hence, isn’t one way the theorem fails in real life is that people’s priors are not partitional? Or does this fall into the auspice of rationality? Is this the same irrationality as not being able to compute the posterior correctly? Thanks in advance.
Comment #113 November 29th, 2015 at 12:09 pm
Hi Scott,
Here’s a really simple example, involving two agents who have a common prior, but nevertheless agree to disagree. The reason they can agree to disagree is that they don’t commonly know that they have a common prior. Examples like this one make me wonder whether the hypotheses of the agreement theorem even apply to ideally rational agents — since a rational agent could fail to know that another person is rational.
There are four worlds — Best, Good, Medium and Bad — and two agents — Alice and Bob. The “Perfect” prior over these worlds is 1/3, 1/6, 1/6, 1/3. The “Imperfect” prior is 1/6, 1/3, 1/3, 1/6. (The first has the 1/6ths on the “inside” worlds Good and Medium, the other has them on the “outside” worlds Best and Bad.)
The agents have different priors at different worlds. If the world is Best or Good, Alice has the Perfect prior. If the world is Medium or Bad, she has the Imperfect Prior. Bob always has the Perfect prior. So if the world is Best or Good, then the agents have a common prior.
As usual, the agents also know different things at different worlds. If the world is Best or Good, Alice knows that it’s Best or Good. If the world is Medium or Bad, Alice knows that it’s Medium or Bad. Bob never learns anything.
At every state — even the ones where they have a common prior — the agents commonly know that Alice’s posterior in the event {Good, Bad} is 1/3. Meanwhile they commonly know that Bob’s posterior in the event {Good, Bad} is 1/2. So they agree to disagree.
At states Best and Good, the agents in fact have a common prior but they don’t know that they do. We can cook up models where they do know, and know that they know…that they have a common prior, for any finite number of iterations of “know that they know”, but still agree to disagree. In fact we can also give examples where they commonly know that they have the same prior, but still agree to disagree because they don’t commonly know which exact distribution is the prior they share.
The hypotheses of the Agreement theorem can also be weakened in several other realistic ways, and under almost any such weakening the theorem ceases to hold! If you’d like a catalog of such counterexamples, you can check out the paper mentioned in comment 88.
Harvey
Comment #114 January 1st, 2016 at 1:30 am
[…] Common knowledge and Aumann’s Agreement Theorem […]
Comment #115 May 23rd, 2016 at 5:26 pm
Dear Scott,
Thank you for this post and it help me greatly to understand common knowledge. I also read Aumann’s paper but can not understand the proof part. Why two people with the same prior, will have the same posterior of a ‘common knowledge’? Also I am unclear about the terminology here. What do prior and posterior exact refer?
Matching with your post, it is following paragraph:
“Now, if Alice’s expectation of a random variable X is common knowledge between her and Bob, that means that everywhere in S, her expectation must be constant … and hence must equal whatever the expectation is, over all the worlds in S! Likewise, if Bob’s expectation is common knowledge with Alice, then everywhere in S, it must equal the expectation of X over S. But that means that Alice’s and Bob’s expectations are the same.”
I don’t understand the idea here, maybe someone could explain more on this point.
Thanks
Comment #116 June 7th, 2016 at 7:20 pm
[…] Trump is unqualified to be President, so the challenge is “just” to make that fact common knowledge (i.e., to ensure everyone knows everyone knows it, everyone knows everyone knows everyone knows it, […]