1. Introduction
Since so little is known about consciousness, it often seems that one can make any assertion about it that one wishes without fear of being proven wrong. For example, one could claim that the true seat of consciousness is an invisible cashew residing in the pancreas, and challenge scientists to find a better explanation. Or one could speculate that consciousness arises from as-yet-undiscovered noncomputable laws of quantum gravity operating within brain structures called microtubules, as Sir Roger Penrose did in his 1994 book Shadows of the Mind [Pen94]. Yet there's one seldom-discussed fact that tells us something tangible and important about consciousness, and that's easily seen to be true. It's that consciousness is finite.
Now we know that the brain is a finite physical object, containing roughly 100 million neurons and 100 billion synapses linking the neurons together. But by consciousness being finite, I mean something stronger: that there are only finitely many lives that could possibly be lived; and that therefore free will, if it exists, must at some level be simply the selection of an element from a finite set. The goals of this article are threefold: to show that this proposition is true; to discuss how it affects Penrose's theory of consciousness; and finally to explain why we needn't worry about the finiteness of our minds.
2. Finiteness
Perhaps you have the sensation of being able to do infinitely many things with your computer. You can visit web sites dealing with medieval weapons or the flammability of Pop Tarts; you can play Minesweeper or Quake, or make the mouse pointer dance across the screen, or write a program or an article about consciousness -- surely this variety has no end? But on closer thought, your computer is a finite object. If it can store N bits of information in memory (where maybe N >> 500 million), then it has at most 2N possible states, and its state at any time is a deterministic function of its previous state and the current input. (Here 'input' refers not only to the keyboard, mouse, microphone, and so forth, but also to the hard disk, CD and floppy drives, internal clock, and any other device external to the processor and memory.) In other words, your computer is what's called a finite-state automaton, or FSA (see Hayes [Hay95]).
Furthermore, time for your computer is broken up into discrete units, so that viewed as an FSA, it might only have, say, 200 million opportunities per second to change state. So clearly there's some finite upper bound M on the number of state transitions your computer can make before it breaks down. To be conservative, we could set M equal to a billion billion billion billion billion (1045), which is many more state transitions than your computer could make between now and when the universe collapses in a Big Crunch or degenerates in a black hole era. Then, raising the number of possible states to the power of M gives us a crude upper bound on how many things your computer could do. It's not infinite; it's at most 2MN.
Here's a disconcerting implication: if you have friends with whom you've only interacted online, then the whole history of your interactions can be described by one of those 2MN possibilities. So in that sense, you're not 'creating' your online conversations; you're just choosing from a large but finite space of pre-existing conversations. The same is true of phone conversations carried over digital switches. As Richard Dawkins [Daw95, p. 14] put it,
"When you plead with your lover over the telephone, every nuance, every catch in the voice, every passionate sigh and yearning timbre is carried along the wire solely in the form of numbers. You can be moved to tears by numbers -- provided they are encoded and decoded fast enough."
To which I'd add that yearning timbres can be encoded not only by numbers, but by numbers of bounded size -- that is, by finitely many of them.
These considerations apply not only to conversations, but to any information that you could store on your computer. The complete works of Shakespeare downloaded from Project Gutenberg, the Mona Lisa stored as a high-resolution JPEG image, and Beethoven's 5th Symphony stored as an MP3 audio file are all just selections from the space of 2MN possibilities. This raises an interesting question: how can 'artistic creativity' exist if every work of art is just a selection among finitely many pre-existing forms? It certainly wouldn't be 'creativity' if, presented with a bag of jellybeans, you chose a red one. I'll return to the matter in Section 5.
For now, let's ask how far our 'finitizing' of human experience can go. We've seen that there are only finitely many phone conversations that could be carried over a digital switch. But what about conversations over an analog switch? Or face-to-face conversations? First kisses? Walks through the park on an autumn day? I argue that there are only finitely many possibilities for each of these things, and indeed for all of human experience. This requires only that a computer could, in principle, simulate a human's experience of the world such that it would be impossible for the human to tell the difference from the real thing -- in other words, that 'total-immersion virtual reality' is theoretically possible. First, note that there's some finite upper bound T on how long any human could live. Again, to be conservative, we can set T equal to 101000 seconds (>> 10992.5 years). Second, at each moment, the human's brain can accept only a finite number A of possible inputs (i.e. signals to the visual, auditory, olfactory, and somatosensory cortexes), and produce only a finite number B of possible outputs (i.e. signals from the motor cortex). But how many 'moments' K are there in a second? Neurons can fire at most around once per millisecond, so as far as the brain's concerned, probably K < 1000. But once again, we'll be conservative, and assume that K = 101000. (Indeed, according to quantum theory, time itself might not be divisible beyond the Planck scale of 10-43 seconds.) Then the total number of human lives that could be lived is at most (AB)KT. This argument doesn't depend on how consciousness works: even if there's an immaterial soul, it can still make at most (AB)KT choices.
3. The Fallacy of the Virtually Infinite
You might object that, even if there are a finite number of phone conversations that could be had, paintings that could be painted, and human lives that could be lived, the numbers are so astronomical that it would make no difference if they were infinite. This objection illustrates what might be called the 'fallacy of the virtually infinite': the conflation of the distinct concepts of 'arbitrarily large' and 'infinite.' That we humans regularly commit this fallacy is understandable: the ability to distinguish between, say, eight goats and ten goats undoubtedly carried an evolutionary advantage, but a prehistoric human who pondered the difference between 101000 goats and infinitely many goats would only be wasting valuable hunting time. And in informal remarks about the vastness of space or of Bill Gates' wealth, we all understand 'virtually infinite' means. But in serious discourse, the fallacy of the virtually infinite can only create confusion. To explain why, we need to talk about sets.
Mathematicians denote the cardinality (or size) of the set of whole numbers,
which is usually what we mean by 'infinity,' as 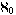 (pronounced aleph-null).
(pronounced aleph-null). 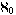 is not a number, nor is there any sense in
which it can be considered the 'largest quantity.' In the 1880's, Georg Cantor
showed that given any set S (which might be infinite), one can form a larger set
by taking the set of subsets of S. The study of higher orders of infinity led to
the amazing theorem of Kurt Gödel (1938) and Paul Cohen (1963) that whether
there are orders of infinity between
is not a number, nor is there any sense in
which it can be considered the 'largest quantity.' In the 1880's, Georg Cantor
showed that given any set S (which might be infinite), one can form a larger set
by taking the set of subsets of S. The study of higher orders of infinity led to
the amazing theorem of Kurt Gödel (1938) and Paul Cohen (1963) that whether
there are orders of infinity between 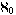 and
the cardinality of real numbers is undecidable within the usual axioms of set
theory [Coh66], but I digress. What's relevant for us is that it's easy to prove
that
and
the cardinality of real numbers is undecidable within the usual axioms of set
theory [Coh66], but I digress. What's relevant for us is that it's easy to prove
that 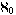 is the lowest order of infinity -- that
is, that there are no sets straddling the fence between finite and infinite
cardinality. This means that there's a sharp distinction between sets of size N,
where N could be an arbitrarily large integer, and infinite sets. These two
classes of sets have very different properties: an infinite set can be placed in
one-to-one correspondence with a proper subset of itself (think of the whole
numbers and the even whole numbers), but this isn't the case for any finite set,
no matter how large.
is the lowest order of infinity -- that
is, that there are no sets straddling the fence between finite and infinite
cardinality. This means that there's a sharp distinction between sets of size N,
where N could be an arbitrarily large integer, and infinite sets. These two
classes of sets have very different properties: an infinite set can be placed in
one-to-one correspondence with a proper subset of itself (think of the whole
numbers and the even whole numbers), but this isn't the case for any finite set,
no matter how large.
The ancient Greeks were suspicious of infinity because of 'paradoxes' related to the Fallacy of the Virtually Infinite, and because of their suspicion humanity had to wait two millennia for Isaac Newton and Gottfried Leibniz to discover differential calculus. But you can avoid the fallacy by remembering this simple rule: that for every whole number N, there are infinitely many whole numbers larger than N. This rule implies that 2, 17, and the number of possible human life experiences are all equally distant from infinity.
4. Implications for Penrose's Argument
When Penrose asserts that consciousness arises from noncomputable processes in the brain, he means that these processes can't be simulated by a Turing machine. The Turing machine is a model of computation proposed by the English mathematician Alan Turing in 1936. At first it seems bizarre: it involves a tape head moving back and forth, reading and writing symbols, on an infinitely long paper tape divided into squares. But the Turing machine can simulate all other models of computation that have ever been proposed, leading to the Church-Turing Thesis, that 'computable by a Turing machine' is what we mean by the word 'computable.' But are any problems noncomputable? Turing proved that the answer is yes. One example is the Halting Problem: given a Turing machine M and an input I, decide whether M will ever stop running when I is the initial configuration of symbols on M's tape. (If there were a Turing machine that decided this problem, we could use it to create another Turing machine H that stops running if its input program P runs forever when run with itself as input, and runs forever if P ever stops running when run with itself as input. Then we could run H with itself as input, creating a contradiction.) Penrose contends that simulating the human mind is among these noncomputable problems, and this is the basis for his speculations about quantum gravity and microtubules. Before we look at why the finiteness of our minds causes problems for Penrose's contention, let's examine his original reason for making it, which is based on Gödel's incompleteness theorem.
The incompleteness theorem says roughly that given any formal proof system F that allows reasoning about numbers and that's consistent (i.e., doesn't allow falsehoods to be proved), there's a statement of F, called G(F), which is true for F and yet unprovable within F. Gödel constructed G(F) by starting with the statement "This statement doesn't have a proof in F," which we can easily see is both true and unprovable in F given that F is consistent. He then showed how to express this statement in the language of F, by encoding the concepts of 'statement' and 'proof' as numbers. Gödel's result is a cornerstone of mathematical logic, but Penrose argues that it's relevant for consciousness as well. His reasoning is that, while a computer operating within the fixed formal system F can't prove G(F), a human can see its truth, and therefore humans must have mental capabilities beyond those of computers.
This argument isn't new (it goes back at least to John Lucas in 1961), and logicians and computer scientists have pointed out a major flaw in it. This is that human mathematicians don't use any consistent formal system such as F: they rely on intuition, and they frequently make mistakes. If we grant a computer this same liberty to make mistakes, then it need not operate strictly within F, and there's nothing paradoxical about it being able to 'see' the truth of G(F). Even without this consideration, that a computer is algorithmic doesn't imply that it must or should use a consistent formal system: if we program it to print '1+1=3,' then it will oblige. Penrose is aware of this flaw, and he tries at great length in Shadows of the Mind to repair it. For example, he argues that, even if individual mathematicians make mistakes, the mathematical community as a whole never disagrees 'in principle' about whether a given statement has been established as true -- but of course it does, in practice! He also asserts that we can distinguish between human mathematicians' 'correctable' mistakes and their 'unassailable' conclusions, but he's never explicit about how we can do so. (See McDermott [McD95].)
But refuting Penrose's argument is like a refuting a proposed method for squaring the circle: although finding the specific flaw can be instructive, we can decide before even looking at the argument that there must be a flaw somewhere. This is because, as we've seen, a human mind accepts only a bounded number of input bits and produces only a bounded number of output bits. So we don't even need the full power of a Turing machine to simulate a mind: a finite-state automaton (as from Section 2) will suffice. This makes the idea that the mind has noncomputational capabilities problematic. Before we consider Penrose's response to this objection, let's look at his proposed taxonomy of views on conscious awareness [Pen94, p. 12]:
- All thinking is computation; in particular, feelings of conscious awareness are evoked merely by the carrying out of appropriate computations.
- Awareness is a feature of the brain's physical action; and whereas any physical action can be simulated computationally, computational simulation cannot by itself evoke awareness.
- Appropriate physical action of the brain evokes awareness, but this physical action cannot even be properly simulated computationally.
- Awareness cannot be explained by physical, computational, or any other scientific terms.
Views A and B, I think, are the ones compatible with the knowledge that consciousness is finite. Penrose states, unsurprisingly, that view C "is the one which I believe myself to be closest to the truth" [Pen94, p. 15]. (He states at the outset that his focus is on explanations for consciousness that at least attempt to be scientific, thus ruling out view D.) The closest Penrose comes to addressing the objection that consciousness is finite is in his 'Q7' (one of twenty objections he raises against his theory, together with his responses). Though Q8 also deals with the fact that computers and brains are finite, it involves mathematical issues that are less relevant to us here. So let's look at Q7 [Pen94, p. 82-83]:
The total output of all the mathematicians who have ever lived, together with the output of all the human mathematicians of the next (say) thousand years is finite and could be contained in the memory banks of an appropriate computer. Surely this particular computer could, therefore, simulate this output and thus behave (externally) in the same way as a human mathematician -- whatever the Gödel argument might appear to tell us to the contrary?
To which Penrose responds, in part:
… One could equally well envisage computers that contain nothing but lists of totally false mathematical 'theorems', or lists containing random jumbles of truths and falsehoods. How are we to tell which computer to trust? The arguments that I am trying to make here do not say that an effective simulation of the output of conscious human activity (here mathematics) is impossible, since purely by chance the computer might 'happen' to get it right -- even without any understanding whatsoever. But the odds against this are absurdly enormous, and the issues that are being addressed here, namely how one decides which mathematical statements are true and which are false, are not even being touched by Q7. [All italics Penrose's]
This sounds like view B, directly contradicting Penrose's stated belief in view C. Penrose might respond by emphasizing the word 'properly' in view C, and arguing that simulating a mind by simply listing each of its finitely many contingencies, together with its chosen responses, isn't a 'proper' simulation. But in that case, why does he even distinguish between views B and C? (Penrose further blurs his stated position in a fantasy dialogue [Pen94, p. 179-190] between a human and a robot. The robot is driven insane when the human challenges it to prove a statement corresponding to G(F), but that the robot can hold an articulate conversation at all would seem to indicate Penrose's agreement with views A or B.) Penrose may not have sufficiently considered the impact that the finiteness of our minds has on his theory.
5. Why Finiteness Isn't So Bad
We've argued that, regardless of whether consciousness arises from the brain's complexity, or an incorporeal soul, or even quantum gravity and microtubules, to be conscious ultimately means to select one element from a finite set. Does this render consciousness trivial? Given the emphasis of 19th-century mathematics on continuous relationships and infinite sets, a mathematician from that era might have answered yes. But since then, it's become increasingly clear that finiteness doesn't imply triviality. The computer scientist Donald Knuth [Knu76] wrote,
"Since the time of Greek philosophy, scholars have prided themselves on their ability to understand something about infinity; and it has become traditional in some circles to regard finite things as essentially trivial, too limited to be of any interest. It is hard to debunk such a notion, since there are no accepted standards for demonstrating that something is interesting, especially when something finite is compared with something transcendent. Yet I believe that the climate of thought is changing, since finite processes are proving to be such fascinating objects of study."
So how did finite objects, dismissed as insignificant less than a century ago, come to take their proper place at the mathematical table? Part of the explanation might lie with Paul Erdös, a giant of 20th-century mathematics, who through his more than 1,500 publications helped bring respectability to the study of graphs and other finite combinatorial objects. The field of finite groups may also have played a role. For example, a group called 'The Monster' has only 8 * 1053 elements, and thus could be completely described by a finite table, but because of its connections to fields such as modular functions and string theory, it occupied the attention of some mathematicians for years.
The greatest impetus, though, has been the computer, which has fueled the creation of whole new branches of finite mathematics. One of these branches, called complexity theory, deals with how quickly the time and memory required to solve a problem grows as a function of the problem's size. For example, in the Maximum Clique problem, we're given a list of N people, together with a list of who's friends with whom, and are asked to find the size of the largest group of people who are all friends with one another. We can solve any instance of Maximum Clique by examining finitely many groups of people (there are 2N possibilities), and thus the problem might seem trivial. But 2N grows so rapidly that when, say, N >> 500, solving the problem by this brute-force approach would take all of the computers in the world today longer than the age of the universe. Maximum Clique is called an NP-complete problem (NP standing for Nondeterministic Polynomial), and thousands of other problems proven to be NP-complete are plagued by this same exponential growth. It's known that if there's an efficient algorithm for any NP-complete problem, then there are efficient algorithms for all of them -- where efficient is defined as requiring an amount of time that's bounded by a polynomial function (say N3) in the size N of the input. Having searched in vain for such an efficient algorithm for decades, complexity theorists assume that no such algorithm exists, and this is called the P!=NP conjecture. Proving (or disproving) P!=NP is one of the great open problems of modern mathematics, with applications to engineering, operations research, cryptography, and even the nature of creativity.
This last claim might seem surprising, especially given Penrose's guess that "the issues of complexity theory are not quite the central ones in relation to mental phenomena" [Pen89, p. 145]. So let's elaborate. Recall that in Section 2, we asked how a work of art could be 'creative' if it's just a selection among finitely many pre-existing possibilities. The answer most people would give, I think, is that if a set of possibilities is so enormous that no two people would ever be likely to make the same choice, then selecting one possibility could be creative. So choosing a jellybean from a bag containing eight flavors wouldn't be creative, but choosing one from a bag containing 101000 flavors might be. Often we're confronted with many more choices than 101000 when we write a poem, compose a song, or draw a picture, because the number of choices grows exponentially with the number of characters, notes, or pixels. But having exponentially many choices, by itself, doesn't guarantee that creativity is possible. We also need that given any choice, evaluating that choice's 'beauty' is computationally intractable -- requiring us to, say, simulate an entire human brain to gauge its reaction to the choice. For if there were an efficient (polynomial-time) algorithm for evaluating artistic beauty, and if complexity theorists ever discovered that P=NP, then art would be rendered trivial! We could have software to write 'optimal' poems, compose 'optimal' songs, and paint 'optimal' pictures, and artists in those fields would be out of jobs. Since we hardly want our notion of creativity to hinge on the solution to an unsolved math problem, we should at least require that evaluating a work of art of size N requires an amount of time exponential in N, and maybe even require the problem to be undecidable. (Humans, of course, could make 'heuristic' judgments of beauty much more efficiently than this.) Thus, even though art only involves selecting among finitely many choices, complexity theory helps us understand that the choice can be nontrivial in practice.
That our minds are finite helps to shed light on certain philosophical arguments, such as Penrose's. But as we've seen, it doesn't render consciousness trivial, nor does it diminish the role of creativity. So I don't mind that my entire life can be modeled by the choosing of a single element from a finite set, and I hope you don't mind that yours can be so modeled either. The finiteness of our minds may even be cause for optimism, because it makes our ability to contemplate the infinite even more astounding.
References
[Coh66] Cohen, Paul. Set Theory and The Continuum Hypothesis. Benjamin Books, 1966.
[Daw95] Dawkins, Richard. River Out of Eden. Basic Books, 1995.
[Hay95] Hayes, Brian. "Debugging Myself," American Scientist, September-October 1995.
[Knu76] Knuth, Donald. "Mathematics and Computer Science: Coping With Finiteness," in Selected Papers on Computer Science, CSLI Publications and Cambridge University Press, 1996. Originally published in Science, Volume 194, December 17, 1976.
[McD95] McDermott, Drew. "[STAR] Penrose is wrong," Psyche, September 22, 1995.
[Pen94] Penrose, Roger. Shadows of the Mind. Oxford University Press, 1996 (first printing 1994).
[Pen89] Penrose, Roger. The Emperor's New Mind. Penguin, 1991 (first printing 1989).