Why have so many great thinkers found quantum mechanics so hard to swallow? To hear some people tell it, the whole source of the trouble is that "God plays dice with the universe" -- that whereas classical mechanics could in principle predict the fall of every sparrow, quantum mechanics gives you only statistical predictions.
Well, you know what? Whup-de-f@#%ing-doo! If indeterminism were the only mystery about quantum mechanics, quantum mechanics wouldn't be mysterious at all. We could imagine, if we liked, that the universe did have a definite state at any time, but that some fundamental principle (besides the obvious practical difficulties) kept us from knowing the whole state. This wouldn't require any serious revision of our worldview. Sure, "God would be throwing dice," but in such a benign way that not even Einstein could have any real beef with it.
The real trouble in quantum mechanics is not that the future trajectory of a particle is indeterministic -- it's that the past trajectory is also indeterministic! Or more accurately, the very notion of a "trajectory" is undefined, since until you measure, there's just an evolving wavefunction. And crucially, because of the defining feature of quantum mechanics -- interference between positive and negative amplitudes -- this wavefunction can't be seen as merely a product of our ignorance, in the same way that a probability distribution can.
Today I want to tell you about decoherence and hidden-variable theories, which are two kinds of stories that people tell themselves to feel better about these difficulties.
The hardheaded physicist will of course ask: given that quantum mechanics works, why should we waste our time trying to feel better about it? Look, if you teach an introductory course on quantum mechanics, and the students don't have nightmares for weeks, tear their hair out, wander around with bloodshot eyes, etc., then you probably didn't get the point across. So rather than deny this aspect of quantum mechanics -- rather than cede the field to the hucksters and charlatans -- shouldn't we map it out ourselves, even sell tickets to the tourists? I mean, if you're going to leap into the abyss, better you should go with an experienced guide who's already been there and back.
Into the Abyss
Alright, so consider the following thought experiment. Let |R⟩ be a state of all the particles in your brain, that corresponds to you looking at a red dot. Let |B⟩ be a state that corresponds to you looking at a blue dot. Now imagine that, in the far future, it's possible to place your brain into a coherent superposition of these two states:
At least to a believer in the Many-Worlds Interpretation, this experiment should be dull as dirt. We've got two parallel universes, one where you see a red dot and the other where you see a blue dot. According to quantum mechanics, you'll find yourself in the first universe with probability |3/5|2=9/25, and in the second universe with probability |4/5|2=16/25. What's the problem?
Well, now imagine that we apply some unitary operation to your brain, which changes its state to
Still a cakewalk! Now you see the red dot with probability 16/25 and the blue dot with probability 9/25.
Aha! But conditioned on seeing the red dot at the earlier time, what's the probability that you'll see the blue dot at the later time?

In ordinary quantum mechanics, this is a meaningless question! Quantum mechanics gives you the probability of getting a certain outcome if you make a measurement at a certain time, period. It doesn't give you multiple-time or transition probabilities -- that is, the probability of an electron being found at point y at time t+1, given that had you measured the electron at time t (which you didn't), it "would have" been at point x. In the usual view, if you didn't actually measure the electron at time t, then it wasn't anywhere at time t: it was just in superposition. And if you did measure it at time t, then of course that would be a completely different experiment!
But why should we care about multiple-time probabilities? For me, it has to do with the reliability of memory. The issue is this: does the "past" have any objective meaning? Even if we don't know all the details, is there necessarily some fact-of-the-matter about what happened in history, about which trajectory the world followed to reach its present state? Or does the past only "exist" insofar as it's reflected in memories and records in the present?
The latter view is certainly the more natural one in quantum mechanics. But as John Bell pointed out, if we take it seriously, then it would seem difficult to do science! For what could it mean to make a prediction if there's no logical connection between past and future states -- if by the time you finish reading this sentence, you might as well find yourself deep in the Amazon rainforest, with all the memories of your trip there conveniently inserted, and all the memories of sitting at a computer reading quantum computing lecture notes conveniently erased?
(Still here? Good!)
Look, we all have fun ridiculing the creationists who think the world sprang into existence on October 23, 4004 BC at 9AM (presumably Babylonian time), with the fossils already in the ground, light from distant stars heading toward us, etc. But if we accept the usual picture of quantum mechanics, then in a certain sense the situation is far worse: the world (as you experience it) might as well not have existed 10-43 seconds ago!
Story #1: Decoherence
The standard response to these difficulties appeals to a powerful idea called decoherence. Decoherence tries to explain why we don't notice "quantum weirdness" in everyday life -- why the world of our experience is a more-or-less classical world. From the standpoint of decoherence, sure there might not be any objective fact about which slit an electron went through, but there is an objective fact about what you ate for breakfast this morning: the two situations are not the same!
The basic idea is that, as soon as the information encoded in a quantum state "leaks out" into the external world, that state will look locally like a classical state. In other words, as far as a local observer is concerned, there's no difference between a classical bit and a qubit that's become hopelessly entangled with the rest of the universe.
So for example, suppose we have a qubit in the state
And suppose this qubit becomes entangled with a second qubit, to form the following joint state:
If we now ignore the second qubit and look only at the first qubit, the first qubit will be in what physicists call the maximally mixed state:
(Other people just call it a classical random bit.) In other words, no matter what measurement you make on the first qubit, you'll just get a random outcome. You're never going to see interference between the |00⟩ and |11⟩ "branches" of the wavefunction. Why? Because according to quantum mechanics, two branches will only interfere if they become identical in all respects. But there's simply no way, by changing the first qubit alone, to make |00⟩ identical to |11⟩. The second qubit will always give away our would-be lovers' differing origins.
To see an interference pattern, you'd have to perform a joint measurement on the two qubits together. But what if the second qubit was a stray photon, which happened to pass through your experiment on its way to the Andromeda galaxy? Indeed, when you consider all the junk that might be entangling itself with your delicate experiment -- air molecules, cosmic rays, geothermal radiation ... well, whatever, I'm not an experimentalist -- it's as if the entire rest of the universe is constantly trying to "measure" your quantum state, and thereby force it to become classical! Sure, even if your quantum state does collapse (i.e. become entangled with the rest of the world), in principle you can still get the state back -- by gathering together all the particles in the universe that your state has become entangled with, and then reversing everything that's happened since the moment of collapse. That would be sort of like Pamela Anderson trying to regain her privacy, by tracking down every computer on Earth that might contain photos of her!
If we accept this picture, then it explains two things:
So, what about the thought experiment from before -- the one where we place your brain into coherent superpositions of seeing a blue dot and seeing a red dot, and then ask about the probability that you see the dot change color? From a decoherence perspective, the resolution is that the thought experiment is completely ridiculous, since brains are big, bulky things that constantly leak electrical signals, and therefore any quantum superposition of two neural firing patterns would collapse (i.e., become entangled with the rest of the universe) in a matter of nanoseconds.
Fine, a skeptic might retort. But what if in the far future, it were possible to upload your entire brain into a quantum computer, and then put the quantum computer into a superposition of seeing a blue dot and seeing a red dot? Huh? Then what's the probability that "you" (i.e. the quantum computer) would see the dot change color?
When I put this question to John Preskill years ago, he said that decoherence itself -- in other words, an approximately classical universe -- seemed to him like an important component of subjective experience as we understand it. And therefore, if you artificially removed decoherence, then it might no longer make sense to ask the same questions about subjective experience that we're used to asking. I'm guessing that this would be a relatively popular response, among those physicists who are philosophical enough to say anything at all.
Decoherence and the Second Law
We are going to get to hidden variables. But first, I want to say one more thing about decoherence.
When I was talking before about the fragility of quantum states -- how they're so easy to destroy, so hard to put back together -- you might have been struck by a parallel with the Second Law of Thermodynamics. Obviously that's just a coincidence, right? Duhhh, no. The way people think about it today, decoherence is just one more manifestation of the Second Law.
Let's see how this works. Given a probability distribution D=(p1,...,pN), recall that the entropy of D is
Then given a quantum mixed state ρ, the von Neumann entropy of ρ is defined to be the minimum, over all unitary transformations U, of the entropy of the probability distribution that results from measuring UρU-1 in the standard basis. To illustrate, every pure state has an entropy of 0, whereas the one-qubit maximally mixed state has an entropy of 1.
Now, if we assume that the universe is always in a pure state, then the "entropy of the universe" starts out 0, and remains 0 for all time! On the other hand, the entropy of the universe isn't really what we care about -- we care about the entropy of this or that region. And we saw before that, as previously-separate physical systems interact with each other, they tend to evolve from pure states into mixed states -- and therefore their entropy goes up. In the decoherence perspective, this is simply the Second Law at work.
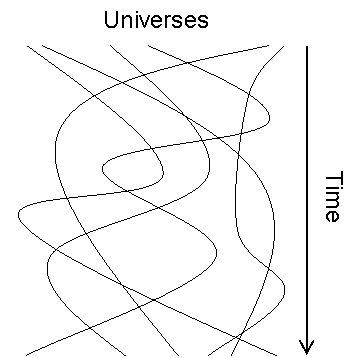
Another way to understand the relationship between decoherence and the Second Law, is by taking a "God's-eye view" of the entire multiverse. Generically speaking, the different branches of the wavefunction could be constantly interfering with each other, splitting and merging in a tangled bush:
What decoherence theory says is that in the real world, the branches look more like a nicely pruned tree:
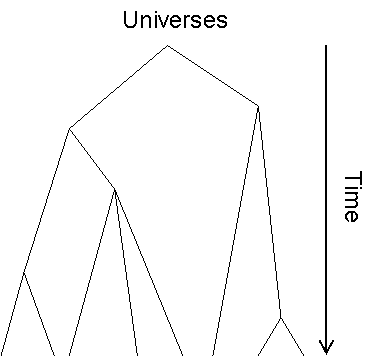
In principle, any two branches of this tree could collide with each other, thereby leading to "macroscopic interference effects," like in my story with the blue and red dots. But in practice, this is astronomically unlikely -- since to collide, two branches would have to become identical in every respect.
Notice that if we accept this tree picture of multiverse, then it immediately gives us a way to define the "arrow of time" -- that is, to state non-circularly what the difference is between the future and the past. Namely, we can say that the past is the direction toward the root of the "multiverse tree," and the future is the direction toward the leaves. According to the decoherence picture, this is actually equivalent to saying that the future is the direction where entropy increases, and it's also equivalent to saying that the past is the direction we remember while the future is the direction we don't.
The tree picture also lets us answer the conundrums from before about the reliability of memory. According to the tree picture, even though in principle we need not have a unique "past," in practice we usually do: namely, the unique path that leads from the root of the multiverse tree to our current state. Likewise, even though in principle quantum mechanics need not provide multiple-time probabilities -- that is, probabilities for what we're going to experience tomorrow, conditioned on what we're experiencing today -- in practice such probabilities usually make perfect sense, for the same reason they make sense in the classical world. That is, when it comes to transitions between subjective experiences, in practice we're dealing not with unitary matrices but with stochastic matrices.
At this point the sharp-eyed reader might notice a problem: won't the branches have to collide eventually, when the tree "runs out of room to expand"? The answer is yes. Firstly, if the Hilbert space is finite-dimensional, then obviously the parallel universes can only branch off a finite number times before they start bumping into each other. But even in an infinite-dimensional Hilbert space, we need to think of each universe as having some finite "width" (think of Gaussian wavepackets for example), so again we can only have a finite number of splittings.
The answer of decoherence theory is that yes, eventually the branches of the multiverse will start interfering with each other -- just like eventually the universe will reach thermal equilibrium. But by that time we'll presumably all be dead.
Incidentally, the fact that our universe is expanding exponentially -- that there's this vacuum energy pushing the galaxies apart -- seems like it might play an important role in "thinning out the multiverse tree," and thereby buying us more time until the branches start interfering with each other. This is something I'd like to understand better.
Oh, yes: I should also mention the "deep" question that I'm glossing over entirely here. Namely, why did the universe start out in such a low-entropy, unentangled state to begin with? Of course one can try to give an anthropic answer to that question, but is there another answer?
Story #2: Hidden Variables
Despite how tidy the decoherence story seems, there are some people for whom it remains unsatisfying. One reason is that the decoherence story had to bring in a lot of assumptions seemingly extraneous to quantum mechanics itself: about the behavior of typical physical systems, the classicality of the brain, and even the nature of subjective experience. A second reason is that the decoherence story never did answer our question about the probability you see the dot change color -- instead the story simply "pulled a Wittgenstein" (that is, tried to convince us the question was meaningless)!
So if the decoherence story doesn't make you sleep easier, then what else is on offer at the quantum bazaar? Well, now it's the hidden-variable theorists' turn to hawk their wares. (Most of the rest of this lecture will follow my paper Quantum Computing and Hidden Variables.)
The idea of hidden-variable theories is simple. If we think of quantum mechanics as describing this vast roiling ocean of parallel universes, constantly branching off, merging, and cancelling each other out, then we're now going to stick a little boat in that ocean. We'll think of the boat's position as representing the "real," "actual" state of the universe at a given point in time, and the ocean as just a "field of potentialities" whose role is to buffet the boat around. For historical reasons, the boat's position is called a hidden variable -- even though in some sense, it's the only part of this setup that's not hidden! Now, our goal will be to make up an evolution rule for the boat, such that at any time, the probability distribution over possible boat positions is exactly the |ψ|2 distribution predicted by standard quantum mechanics.
By construction, then, hidden-variable theories are experimentally indistinguishable from standard quantum mechanics. So presumably there can be no question of whether they're "true" or "false" -- the only question is whether they're good or bad stories.
You might say, why should we worry about these unfalsifiable goblins hiding in quantum mechanics' closet? Well, I'll give you four reasons.
From my perspective, a hidden-variable theory is simply a rule for converting a unitary transformation into a classical probabilistic transformation. In other words, it's a function that takes as input an N-by-N unitary matrix U=(uij) together with a quantum state
and that produces as output an N-by-N stochastic matrix S=(sij). (Recall that a stochastic matrix is just a nonnegative matrix where every column sums to 1.) Given as input the probability vector obtained from measuring |ψ⟩ in the standard basis, this S should produce as output the probability vector obtained from measuring U|ψ⟩ in the standard basis. In other words, if
then we must have
This is what it means for a hidden-variable theory to reproduce the predictions of quantum mechanics: it means that, whatever story we want to tell about correlations between boat positions at different times, certainly the marginal distribution over boat positions at any individual time had better be the usual quantum-mechanical one.
OK, obvious question: given a unitary matrix U and a state |ψ⟩, does a stochastic matrix satisfying the above condition necessarily exist?
Sure it does! For we can always take the product transformation
which just "picks the boat up and puts it back down at random," completely destroying any correlation between the initial and final positions.
No-Go Theorems Galore
So the question is not whether we can find a stochastic transformation S(|ψ⟩,U) that maps the initial distribution to the final one. Certainly we can! Rather, the question is whether we can find a stochastic transformation satisfying "nice" properties. But which "nice" properties might we want? I'm now going to suggest four possibilities -- and then show that, alas, not one of them can be satisfied. The point of going through this exercise is that, along the way, we're going to learn an enormous amount about how quantum mechanics differs from classical probability theory. In particular, we'll learn about Bell's Theorem, the Kochen-Specker Theorem, and two other no-go theorems that as far as I know don't have names.
1. Independence from the State
Alright, so recall the problem at hand: we're given a unitary matrix U and quantum state |ψ⟩, and want to cook up a stochastic matrix S = S(|ψ⟩,U) that maps the distribution obtained by measuring |ψ⟩ to the distribution obtained by measuring U|ψ⟩.
The first property we might want is that S should depend only on the unitary U, and not on the state |ψ⟩. However, this is easily seen to be impossible. For if we let
then
implies
whereas
implies
Therefore S must be a function of U and |ψ⟩ together.
2. Invariance under Time-Slicings
The second property we might want in our hidden-variable theory is invariance under time-slicings. This means that, if we perform two unitary transformations U and V in succession, we should get the same result if we apply the hidden-variable theory to VU, as if we apply the theory to U and V separately and then multiply the results. (Loosely speaking, the map from unitary to stochastic matrices should be "homomorphic.") Formally, what we want is that
But again one can show that this is impossible -- except in the "trivial" case that S is the product transformation Sprod, which destroys all correlations between the initial and final times.
To see this, observe that for all unitaries W and states |ψ⟩, we can write W as a product W = VU, in such a way that U|ψ⟩ equals a fixed basis state (|1⟩, for example). Then applying U "erases" all the information about the hidden variable's initial value -- so that if we later apply V, then the hidden variable's final value must be uncorrelated with its initial value. But this means that S(|ψ⟩,VU) equals Sprod(|ψ⟩,VU).
3. Independence from the Basis
When I defined hidden-variable theories, some of you were probably wondering: why should we only care about measurement results in some particular basis, when we could've just as well picked any other basis? So for example, if we're going to say that a particle has a "true, actual" location even before anyone measures that location, then shouldn't we say the same thing about the particle's momentum, and its spin, and its energy, and all the other observable properties of the particle? What singles out location as being more "real" than all the other properties?
Well, these are excellent questions! Alas, it turns out that we can't assign definite values to all possible properties of a particle in any "consistent" way. In other words, not only can we not define transition probabilities for all the particle's properties, we can't even handle all the properties simultaneously at any individual time!
This is the remarkable (if mathematically trivial) conclusion of the Kochen-Specker Theorem, which was proved by Simon Kochen and Ernst Specker in 1967. Formally, the theorem says the following: suppose that for every orthonormal basis B in ℜ3, the universe wants to "precompute" what the outcome would be of making a measurement in that basis. In other words, the universe wants to pick one of the three vectors in B, designate that one as the "marked" vector, and return that vector later should anyone happen to measure in B. Naturally, the marked vectors ought to be "consistent" across different bases. That is, if two bases share a common vector, like so:
then the common vector should be the marked vector of one basis if and only if it's also the marked vector of the other.
Kochen and Specker prove that this is impossible. Indeed, they construct an explicit set of 117 bases (!) in ℜ3, such that marked vectors can't be chosen for those bases in any consistent way.
NerdNote: The constant 117 has since been improved to 31; see here for example. Apparently it's still an open problem whether that's optimal; the best lower bound I've seen mentioned is 18.
The upshot is that any hidden-variable theory will have to be what those in the business call contextual. That is, it will sometimes have to give you an answer that depends on which basis you measured in, with no pretense that the answer would've been the same had you measured in a different basis that also contained the same answer.
Exercise: Prove that the Kochen-Specker Theorem is false in 2 dimensions.
4. Relativistic Causality
The final property we might want from a hidden-variable theory is adherence to the "spirit" of Einstein's special relativity. For our purposes, I'll define that to consist of two things:
Now, you might've heard of a little thing called Bell's Inequality. As it turns out, Bell's Inequality doesn't quite rule out hidden-variable theories satisfying the two axioms above, but a slight strengthening of what Bell proved does the trick.
So what is Bell's Inequality? Well, if you look for an answer in almost any popular book or website, you'll find page after page about entangled photon sources, Stern-Gerlach apparatuses, etc., all of it helpfully illustrated with detailed experimental diagrams. This is necessary, of course, since if you took all the complications away, people might actually grasp the conceptual point!
However, since I'm not a member of the Physics Popularizers' Guild, I'm now going to break that profession's time-honored bylaws, and just tell you the conceptual point directly.
We've got two players, Alice and Bob, and they're playing the following game. Alice flips a fair coin; then, based on the result, she can either raise her hand or not. Bob flips another fair coin; then, based on the result, he can either raise his hand or not. What both players want is that exactly one of them should raise their hand, if and only if both coins landed heads. If that condition is satisfied then they win the game; if it isn't then they lose. (This is a cooperative rather than competitive game.)
Now here's the catch: Alice and Bob are both in sealed rooms (possibly even on different planets), and can't communicate with each other at all while the game is in progress.
The question that interests us is: what is the maximum probability with which Alice and Bob can win the game?
Well, certainly they can win 75% of the time. Why?
Right: they can both just decide never to raise their hands, regardless of how the coins land! In that case, the only way they'll lose is if both of the coins land heads.
Exercise: Prove that this is optimal. In other words, any strategy of Alice and Bob will win at most 75% of the time.
Now for the punchline: suppose that Alice and Bob share the entangled state
with Alice holding one half and Bob holding the other half. In that case, there exists a strategy by which they can win the game with probability
To be clear, having the state |Φ⟩ does not let Alice and Bob send messages to each other faster than the speed of light -- nothing does! What it lets them do is to win this particular game more than 75% of the time. Naïvely, we might have thought that would require Alice and Bob to "cheat" by sending each other messages, but that simply isn't true -- they can also cheat by using entanglement!
So that was Bell's Inequality.
But what does this dumb little game have to do with hidden variables? Well, suppose we tried to model Alice's and Bob's measurements of the state |Φ⟩ using two hidden variables: one on Alice's side and the other on Bob's side. And, in keeping with relativistic causality, suppose we demanded that nothing that happened to Alice's hidden variable could affect Bob's hidden variable or vice versa. In that case, we'd predict that Alice and Bob could win the game at most 75% of the time. But this prediction would be wrong!
It follows that, if we want it to agree with quantum mechanics, then any hidden-variable theory has to allow "instantaneous communication" between any two points in the universe. Once again, this doesn't mean that quantum mechanics itself allows instantaneous communication (it doesn't), or that we can exploit hidden variables to send messages faster than light (we can't). It only means that, if we choose to describe quantum mechanics using hidden variables, then our description will have to involve instantaneous communication.
Exercise: Generalize Bell's argument to show that there's no hidden-variable theory satisfying the locality and commutativity axioms as given above.
So what we've learned, from Alice and Bob's coin-flipping game, is that any attempt to describe quantum mechanics with hidden variables will necessarily lead to tension with relativity. Again, none of this has any experimental consequences, since it's perfectly possible for hidden-variable theories to violate the "spirit" of relativity while still obeying the "letter." Indeed, hidden-variable fans like to argue that all we're doing is unearthing the repressed marital tensions between relativity and quantum mechanics themselves!
Examples of Hidden-Variable Theories
I know what you're thinking: after the pummeling we just gave them, the outlook for hidden-variable theories looks pretty bleak. But here's the amazing thing: even in the teeth of four different no-go theorems, one can still construct interesting and mathematically nontrivial hidden-variable theories. I'd like to end this lecture by giving you three examples.
The Flow Theory
Remember the goal of hidden-variable theories: we start out with a unitary matrix U and a state |ψ⟩; from them we want to produce a stochastic matrix S that maps the initial distribution to the final distribution. Ideally, S should be derived from U in a "natural," "organic" way. So for example, if the (i,j) entry of U is zero, then the (i,j) entry of S should also be zero. Likewise, making a small change to U or |ψ⟩ should produce only a small change in S.
Now, it's not clear a priori that there even exists a hidden-variable theory satisfying the two requirements above. So what I want to do first is give you a simple, elegant theory that does satisfy those requirements.
The basic idea is to treat probability mass flowing through the multiverse just like oil flowing through pipes! We're going to imagine that initially, we have |αi|2 units of "oil" at each basis state |i⟩, while by the end, we want |βi|2 units of oil at each basis state |i⟩. Here αi and βi are the initial and final amplitudes of |i⟩ respectively. And we're also going to think of |uij|, the absolute value of the (i,j)th entry of the unitary matrix, as the capacity of an "oil pipe" leading from |i⟩ to |j⟩.
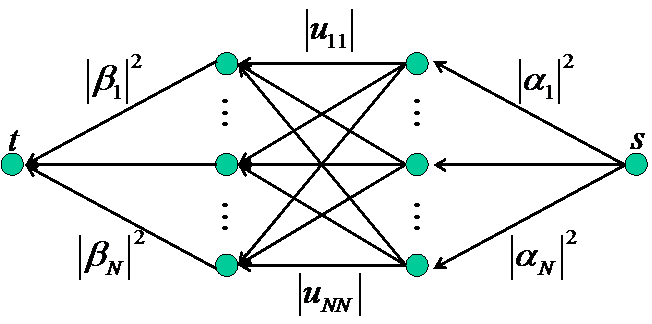
The network G(U,|ψ⟩)
Then the first question is this: for any U and |ψ⟩, can all 1 units of oil be routed from s to t in the above network G(U,|ψ⟩), without exceeding the capacity of any of the pipes?
I proved that the answer is yes. My proof uses a fundamental result from the 1960's called the Max-Flow/Min-Cut Theorem. Those of you who were/are computer science majors will vaguely remember this from your undergrad classes. For the rest of you, well, it's really worth seeing at least once in your life. (It's useful not only for the interpretation of quantum mechanics, but also for stuff like Internet routing!)
So what does the Max-Flow/Min-Cut Theorem say? Well, suppose we have a network of oil pipes like in the figure above, with a designated "source" called s, and a designated "sink" called t. Each pipe has a known "capacity", which is a nonnegative real number measuring how much oil can be sent through that pipe each second. Then the max flow is just the maximum amount of oil that can be sent from s to t every second, if we route the oil through the pipes in as clever a way as possible. Conversely, the min cut is the smallest real number C such that, by blowing up oil pipes whose total capacity is C, a terrorist could prevent any oil from being sent from s to t.
As an example, what's the max flow and min cut for the network below?
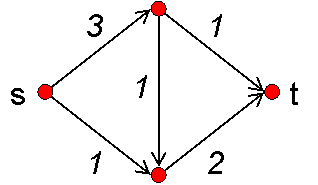
Right: they're both 3.
As a trivial observation, I claim that for any network, the max flow can never be greater than the min cut. Why?
Right: because by definition, the min cut is the total capacity of some "choke point" that all the oil has to pass through eventually! In other words, if blowing up pipes of total capacity C is enough to cut the flow from s to t down to zero, then putting those same pipes back in can't increase the flow to more than C.
Now, the Max-Flow/Min-Cut Theorem says that the converse is also true: for any network, the max flow and min cut are actually equal.
Exercise (for those who've never seen it): Prove the Max-Flow/Min-Cut Theorem.
Exercise (hard): By using the Max-Flow/Min-Cut Theorem, prove that for any unitary U and any state |ψ⟩, there exists a way to route all the probability mass from s to t in the network G(U,|ψ⟩) shown before.
So, we've now got our candidate hidden-variable theory! Namely: given U and |ψ⟩, first find a "canonical" way to route all the probability mass from s to t in the network G(U,|ψ⟩). Then define the stochastic matrix S by sij := pij/|αi|2, where pij is the amount of probability mass routed from |i⟩ to |j⟩. (For simplicity, I'll ignore what happens when αi=0.)
By construction, this S maps the vector of |αi|2's to the vector of |βi|2's. It also has the nice the property that for all i,j, if uij=0 then sij=0 as well.
Right! Because if uij=0, then no probability mass can get routed from |i⟩ to |j⟩.
Exercise (harder): Prove that making a small change to U or |ψ⟩ produces only a small change in the matrix (pij) of transition probabilities.
The Schrödinger Theory
So that was one cute example of a hidden-variable theory. I now want to show you an example that I think is even cuter. When I started thinking about hidden-variable theories, this was actually the first idea I came up with. Later I found out that Schrödinger had the same idea in a nearly-forgotten 1931 paper.
Specifically, Schrödinger's idea was to define transition probabilities in quantum mechanics by solving a system of coupled nonlinear equations. The trouble is that Schrödinger couldn't prove that his system had a solution (let alone a unique one); that had to wait for the work of Masao Nagasawa in the 1980's. Luckily for me, I only cared about finite-dimensional quantum systems, where everything was much simpler, and where I could give a reasonably elementary proof that the equation system was solvable.
So what's the idea? Well, recall that given a unitary matrix U, we want to "convert" it somehow into a stochastic matrix S that maps the initial distribution to the final one. This is basically equivalent to asking for a matrix P of transition probabilities: that is, a nonnegative matrix whose ith column sums to |αi|2 and whose jth row sums to |βj|2. (This is just the requirement that the marginal probabilities should be the usual quantum-mechanical ones.)
Since we want to end up with a nonnegative matrix, a reasonable first step would be to replace every entry of U by its absolute value:
What next? Well, we want the ith column to sum to |αi|2. So let's continue doing the crudest thing imaginable, and for every 1≤i≤N, just normalize the ith column to sum to |αi|2!
Now, we also want the jth row to sum to |βj|2. How do we get that? Well, for every 1≤j≤N, we just normalize the jth row to sum to |βj|2.
Of course, after we normalize the rows, in general the ith column will no longer sum to |αi|2. But that's no problem: we'll just normalize the columns again! Then we'll re-normalize the rows (which were messed up by normalizing the columns), then we'll re-normalize the columns (which were messed up by normalizing the rows), and so on ad infinitum.
Exercise (hard): Prove that this iterative process converges for any U and |ψ⟩, and that the limit is a matrix P=(pij) of transition probabilities -- that is, a nonnegative matrix whose ith column sums to |αi|2 and whose jth row sums to |βj|2.
Open Problem (if you get this, let me know): Prove that making a small change to U or |ψ⟩ produces only a small change in the matrix P=(pij) of transition probabilities.
Bohmian Mechanics
Some of you might be wondering why I haven't mentioned the most famous hidden-variable theory of all: Bohmian mechanics. The answer is that, to discuss Bohmian mechanics, I'd have to bring in infinite-dimensional Hilbert spaces (blech!), particles with positions and momenta (double blech!), and other ideas that go against everything I stand for as a computer scientist.
Still, I should tell you a little about what Bohmian mechanics is and why it doesn't fit into my framework. In 1952, David Bohm proposed a deterministic hidden-variable theory: that is, a theory where not only do you get transition probabilities, but the probabilities are all either 0 or 1! The way he did this was by taking as his hidden variable the positions of particles in ℜ3. He then stipulated that the probability mass for where the particles are should "flow" with the wavefunction, so that a region of configuration space with probability ε always gets mapped to another region with probability ε.
With one particle in one spatial dimension, it's easy to write down the (unique) differential equation for particle position that satisfies Bohm's probability constraint. Bohm showed how to generalize the equation to any number of particles in any number of dimensions.
To illustrate, here's what the Bohmian particle trajectories look like in the famous double-slit experiment:

Again, the amazing thing about this theory is that it's deterministic: specify the "actual" positions of all the particles in the universe at any one time, and you've specified their "actual" positions at all earlier and later times. So if you like, you can imagine that at the moment of the Big Bang, God sprinkled particles across the universe according to the usual |ψ|2 distribution; but after that He smashed His dice, and let the particles evolve deterministically forever after. And that assumption will lead you to exactly the same experimental predictions as the usual picture of quantum mechanics, the one where God's throwing dice up the wazoo.
The catch, from my point of view, is that this sort of determinism can only work in an infinite-dimensional Hilbert space, like the space of particle positions. I've almost never seen this observation discussed in print, but I can explain it in a couple sentences.
Suppose we want a hidden-variable theory that's deterministic like Bohm's, but that works for quantum states in a finite number of dimensions. Then what happens if we apply a unitary transformation U that maps the state |0⟩ to
In this case, initially the hidden variable is |0⟩ with certainty; afterwards it's |0⟩ with probability 1/2 and |1⟩ with probability 1/2. In other words, applying U increases the entropy of the hidden variable from 0 to 1. So to decide which way the hidden variable goes, clearly Nature needs to flip a coin!
A Bohmian would say that the reason determinism broke down here is that our wavefunction was "degenerate": that is, it didn't satisfy the continuity and differentiability requirements that are needed for Bohm's differential equation. But in a finite-dimensional Hilbert space, every wavefunction will be degenerate in that sense! And that's why, if our universe is discrete at the Planck scale, then it can't also be deterministic in the Bohmian sense.
[Discussion of this lecture on blog]