Shtetl-Optimized

Update (Feb. 29): A YouTube video of this talk is now available, plus a comment section filled (as usual) with complaints about everything from my speech and mannerisms to my failure to address the commenter’s pet topic.

Another Update (March 8): YouTube video of a shorter (18-minute) version of this talk, which I delivered at TEDxPaloAlto, is now available as well!

---

Here, as promised in my last post, is a written version of the talk I delivered a couple weeks ago at MindFest in Florida, entitled “The Problem of Human Specialness in the Age of AI.” The talk is designed as one-stop shopping, summarizing many different AI-related thoughts I’ve had over the past couple years (and earlier).

---

1. INTRO

Thanks so much for inviting me! I’m not an expert in AI, let alone mind or consciousness.  Then again, who is?

For the past year and a half, I’ve been moonlighting at OpenAI, thinking about what theoretical computer science can do for AI safety.  I wanted to share some thoughts, partly inspired by my work at OpenAI but partly just things I’ve been wondering about for 20 years.  These thoughts are not directly about “how do we prevent super-AIs from killing all humans and converting the galaxy into paperclip factories?”, nor are they about “how do we stop current AIs from generating misinformation and being biased?,” as much attention as both of those questions deserve (and are now getting).  In addition to “how do we stop AGI from going disastrously wrong?,” I find myself asking “what if it goes right?  What if it just continues helping us with various mental tasks, but improves to where it can do just about any task as well as we can do it, or better?  Is there anything special about humans in the resulting world?  What are we still for?”

---

2. LARGE LANGUAGE MODELS

I don’t need to belabor for this audience what’s been happening lately in AI.  It’s arguably the most consequential thing that’s happened in civilization in the past few years, even if that fact was temporarily masked by various ephemera … y’know, wars, an insurrection, a global pandemic … whatever, what about AI?

I assume you’ve all spent time with ChatGPT, or with Bard or Claude or other Large Language Models, as well as with image models like DALL-E and Midjourney.  For all their current limitations—and we can discuss the limitations—in some ways these are the thing that was envisioned by generations of science fiction writers and philosophers.  You can talk to them, and they give you a comprehending answer.  Ask them to draw something and they draw it.

I think that, as late as 2019, very few of us expected this to exist by now.  I certainly didn’t expect it to.  Back in 2014, when there was a huge fuss about some silly ELIZA-like chatbot called “Eugene Goostman” that was falsely claimed to pass the Turing Test, I asked around: why hasn’t anyone tried to build a much better chatbot, by (let’s say) training a neural network on all the text on the Internet?  But of course I didn’t do that, nor did I know what would happen when it was done.

The surprise, with LLMs, is not merely that they exist, but the way they were created.  Back in 1999, you would’ve been laughed out of the room if you’d said that all the ideas needed to build an AI that converses with you in English already existed, and that they’re basically just neural nets, backpropagation, and gradient descent.  (With one small exception, a particular architecture for neural nets called the transformer, but that probably just saves you a few years of scaling anyway.)  Ilya Sutskever, cofounder of OpenAI (who you might’ve seen something about in the news…), likes to say that beyond those simple ideas, you only needed three ingredients:

(1) a massive investment of computing power,
(2) a massive investment of training data, and
(3) faith that your investments would pay off!

Crucially, and even before you do any reinforcement learning, GPT-4 clearly seems “smarter” than GPT-3, which seems “smarter” than GPT-2 … even as the biggest ways they differ are just the scale of compute and the scale of training data!  Like,

• GPT-2 struggled with grade school math.
• GPT-3.5 can do most grade school math but it struggles with undergrad material.
• GPT-4, right now, can probably pass most undergraduate math and science classes at top universities (I mean, the ones without labs or whatever!), and possibly the humanities classes too (those might even be easier for GPT-4 than the science classes, but I’m much less confident about it). But it still struggles with, for example, the International Math Olympiad.  How insane, that this is now where we have to place the bar!

Obvious question: how far will this sequence continue?  There are certainly a least a few more orders of magnitude of compute before energy costs become prohibitive, and a few more orders of magnitude of training data before we run out of public Internet. Beyond that, it’s likely that continuing algorithmic advances will simulate the effect of more orders of magnitude of compute and data than however many we actually get.

So, where does this lead?

(Note: ChatGPT agreed to cooperate with me to help me generate the above image. But it then quickly added that it was just kidding, and the Riemann Hypothesis is still open.)

---

3. AI SAFETY

Of course, I have many friends who are terrified (some say they’re more than 90% confident and few of them say less than 10%) that not long after that, we’ll get this…

But this isn’t the only possibility smart people take seriously.

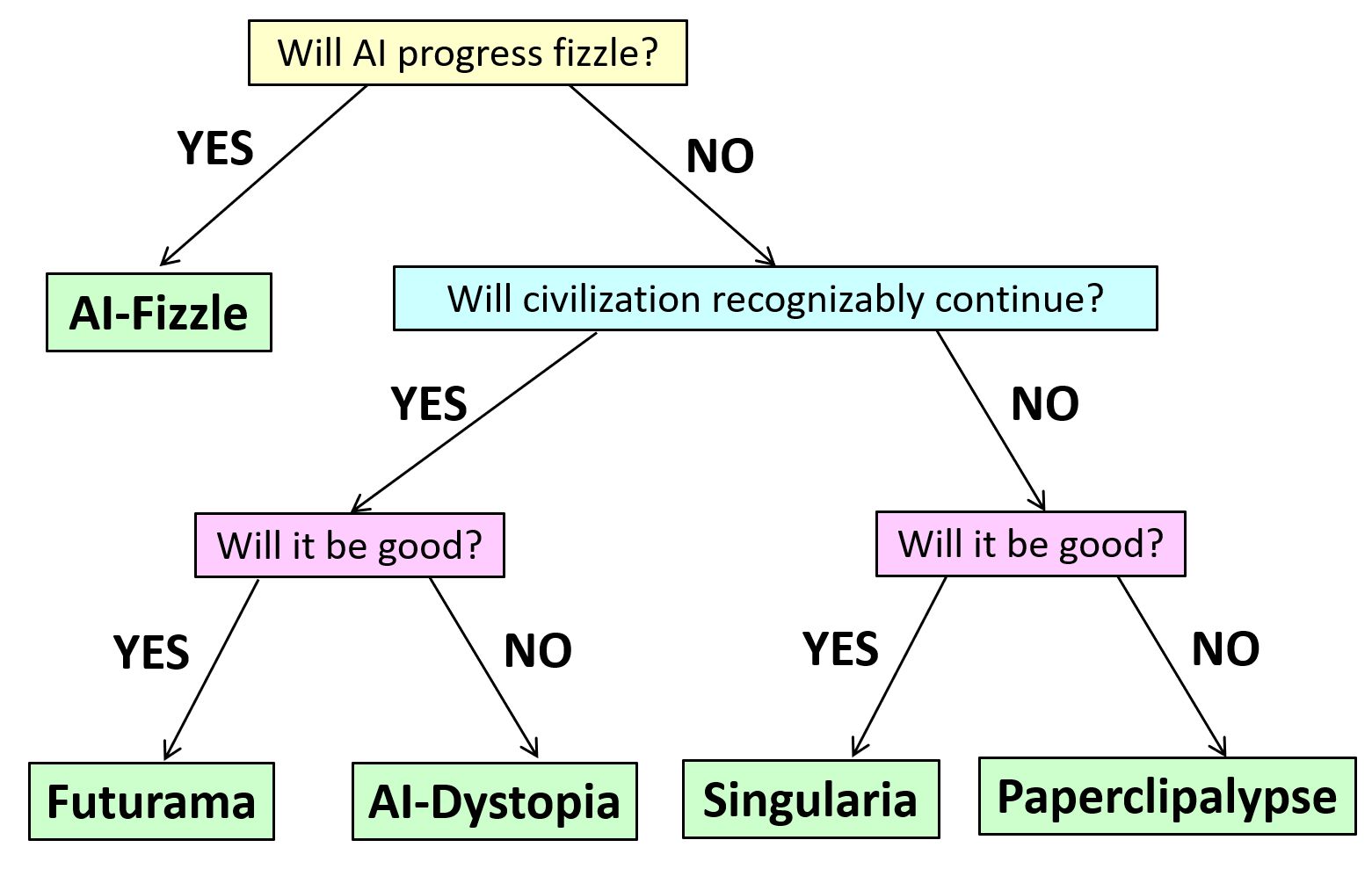
Another possibility is that the LLM progress fizzles before too long, just like previous bursts of AI enthusiasm were followed by AI winters.  Note that, even in the ultra-conservative scenario, LLMs will probably still be transformative for the economy and everyday life, maybe as transformative as the Internet.  But they’ll just seem like better and better GPT-4’s, without ever seeming qualitatively different from GPT-4, and without anyone ever turning them into stable autonomous agents and letting them loose in the real world to pursue goals the way we do.

A third possibility is that AI will continue progressing through our lifetimes as quickly as we’ve seen it progress over the past 5 years, but even as that suggests that it’ll surpass you and me, surpass John von Neumann, become to us as we are to chimpanzees … we’ll still never need to worry about it treating us the way we’ve treated chimpanzees.  Either because we’re projecting and that’s just totally not a thing that AIs trained on the current paradigm would tend to do, or because we’ll have figured out by then how to prevent AIs from doing such things.  Instead, AI in this century will “merely” change human life by maybe as much as it changed over the last 20,000 years, in ways that might be incredibly good, or incredibly bad, or both depending on who you ask.

If you’ve lost track, here’s a decision tree of the various possibilities that my friend (and now OpenAI allignment colleague) Boaz Barak and I came up with.

---

4. JUSTAISM AND GOALPOST-MOVING

Now, as far as I can tell, the empirical questions of whether AI will achieve and surpass human performance at all tasks, take over civilization from us, threaten human existence, etc. are logically distinct from the philosophical question of whether AIs will ever “truly think,” or whether they’ll only ever “appear” to think.  You could answer “yes” to all the empirical questions and “no” to the philosophical question, or vice versa.  But to my lifelong chagrin, people constantly munge the two questions together!

A major way they do so, is with what we could call the religion of Justaism.

• GPT is justa next-token predictor.
• It’s justa function approximator.
• It’s justa gigantic autocomplete.
• It’s justa stochastic parrot.
• And, it “follows,” the idea of AI taking over from humanity is justa science-fiction fantasy, or maybe a cynical attempt to distract people from AI’s near-term harms.

As someone once expressed this religion on my blog: GPT doesn’t interpret sentences, it only seems-to-interpret them.  It doesn’t learn, it only seems-to-learn.  It doesn’t judge moral questions, it only seems-to-judge. I replied: that’s great, and it won’t change civilization, it’ll only seem-to-change it!

A closely related tendency is goalpost-moving.  You know, for decades chess was the pinnacle of human strategic insight and specialness, and that lasted until Deep Blue, right after which, well of course AI can cream Garry Kasparov at chess, everyone always realized it would, that’s not surprising, but Go is an infinitely richer, deeper game, and that lasted until AlphaGo/AlphaZero, right after which, of course AI can cream Lee Sedol at Go, totally expected, but wake me up when it wins Gold in the International Math Olympiad.  I bet $100 against my friend Ernie Davis that the IMO milestone will happen by 2026.  But, like, suppose I’m wrong and it’s 2030 instead … great, what should be the next goalpost be?

Indeed, we might as well formulate a thesis, which despite the inclusion of several weasel phrases I’m going to call falsifiable:

Given any game or contest with suitably objective rules, which wasn’t specifically constructed to differentiate humans from machines, and on which an AI can be given suitably many examples of play, it’s only a matter of years before not merely any AI, but AI on the current paradigm (!), matches or beats the best human performance.

Crucially, this Aaronson Thesis (or is it someone else’s?) doesn’t necessarily say that AI will eventually match everything humans do … only our performance on “objective contests,” which might not exhaust what we care about.

Incidentally, the Aaronson Thesis would seem to be in clear conflict with Roger Penrose’s views, which we heard about from Stuart Hameroff’s talk yesterday.  The trouble is, Penrose’s task is “just see that the axioms of set theory are consistent” … and I don’t know how to gauge performance on that task, any more than I know how to gauge performance on the task, “actually taste the taste of a fresh strawberry rather than merely describing it.”  The AI can always say that it does these things!

---

5. THE TURING TEST

This brings me to the original and greatest human vs. machine game, one that was specifically constructed to differentiate the two: the Imitation Game, which Alan Turing proposed in an early and prescient (if unsuccessful) attempt to head off the endless Justaism and goalpost-moving.  Turing said: look, presumably you’re willing to regard other people as conscious based only on some sort of verbal interaction with them.  So, show me what kind of verbal interaction with another person would lead you to call the person conscious: does it involve humor? poetry? morality? scientific brilliance?  Now assume you have a totally indistinguishable interaction with a future machine.  Now what?  You wanna stomp your feet and be a meat chauvinist?

(And then, for his great attempt to bypass philosophy, fate punished Turing, by having his Imitation Game itself provoke a billion new philosophical arguments…)

---

6. DISTINGUISHING HUMANS FROM AIS

Although I regard the Imitation Game as, like, one of the most important thought experiments in the history of thought, I concede to its critics that it’s generally not what we want in practice.

It now seems probable that, even as AIs start to do more and more work that used to be done by doctors and lawyers and scientists and illustrators, there will remain straightforward ways to distinguish AIs from humans—either because customers want there to be, or governments force there to be, or simply because indistinguishability wasn’t what was wanted or conflicted with other goals.

Right now, like it or not, a decent fraction of all high-school and college students on earth are using ChatGPT to do their homework for them. For that reason among others, this question of how to distinguish humans from AIs, this question from the movie Blade Runner, has become a big practical question in our world.

And that’s actually one of the main things I’ve thought about during my time at OpenAI.  You know, in AI safety, people keep asking you to prognosticate decades into the future, but the best I’ve been able to do so far was see a few months into the future, when I said: “oh my god, once everyone starts using GPT, every student will want to use it to cheat, scammers and spammers will use it too, and people are going to clamor for some way to determine provenance!”

In practice, often it’s easy to tell what came from AI.  When I get comments on my blog like this one:

“Erica Poloix,” July 21, 2023:
Well, it’s quite fascinating how you’ve managed to package several misconceptions into such a succinct comment, so allow me to provide some correction. Just as a reference point, I’m studying physics at Brown, and am quite up-to-date with quantum mechanics and related subjects.

…

The bigger mistake you’re making, Scott, is assuming that the Earth is in a ‘mixed state’ from the perspective of the universal wavefunction, and that this is somehow an irreversible situation. It’s a misconception that common, ‘classical’ objects like the Earth are in mixed states. In the many-worlds interpretation, for instance, even macroscopic objects are in superpositions – they’re just superpositions that look classical to us because we’re entangled with them. From the perspective of the universe’s wavefunction, everything is always in a pure state.

As for your claim that we’d need to “swap out all the particles on Earth for ones that are already in pure states” to return Earth to a ‘pure state,’ well, that seems a bit misguided. All quantum systems are in pure states before they interact with other systems and become entangled. That’s just Quantum Mechanics 101.

I have to say, Scott, your understanding of quantum physics seems to be a bit, let’s say, ‘mixed up.’ But don’t worry, it happens to the best of us. Quantum Mechanics is counter-intuitive, and even experts struggle with it. Keep at it, and try to brush up on some more fundamental concepts. Trust me, it’s a worthwhile endeavor.

… I immediately say, either this came from an LLM or it might as well have.  Likewise, apparently hundreds of students have been turning in assignments that contain text like, “As a large language model trained by OpenAI…”—easy to catch!

But what about the slightly more sophisticated cheaters? Well, people have built discriminator models to try to distinguish human from AI text, such as GPTZero.  While these distinguishers can get well above 90% accuracy, the danger is that they’ll necessarily get worse as the LLMs get better.

So, I’ve worked on a different solution, called watermarking.  Here, we use the fact that LLMs are inherently probabilistic — that is, every time you submit a prompt, they’re sampling some path through a branching tree of possibilities for the sequence of next tokens.  The idea of watermarking is to steer the path using a pseudorandom function, so that it looks to a normal user indistinguishable from normal LLM output, but secretly it encodes a signal that you can detect if you know the key.

I came up with a way to do that in Fall 2022, and others have since independently proposed similar ideas.  I should caution you that this hasn’t been deployed yet—OpenAI, along with DeepMind and Anthropic, want to move slowly and cautiously toward deployment.  And also, even when it does get deployed, anyone who’s sufficiently knowledgeable and motivated will be able to remove the watermark, or produce outputs that aren’t watermarked to begin with.

---

7. THE FUTURE OF PEDAGOGY

But as I talked to my colleagues about watermarking, I was surprised that they often objected to it on a completely different ground, one that had nothing to do with how well it can work.  They said: look, if we all know students are going to rely on AI in their jobs, why shouldn’t they be allowed to rely on it in their assignments?  Should we still force students to learn to do things if AI can now do them just as well?

And there are many good pedagogical answers you can give: we still teach kids spelling and handwriting and arithmetic, right?  Because, y’know, we haven’t yet figured out how to instill higher-level conceptual understanding without all that lower-level stuff as a scaffold for it.

But I already think about this in terms of my own kids.  My 11-year-old daughter Lily enjoys writing fantasy stories.  Now, GPT can also churn out short stories, maybe even technically “better” short stories, about such topics as tween girls who find themselves recruited by wizards to magical boarding schools that are not Hogwarts and totally have nothing to do with Hogwarts.  But here’s a question: from this point on, will Lily’s stories ever surpass the best AI-written stories?  When will the curves cross?  Or will AI just continue to stay ahead?

---

8. WHAT DOES “BETTER” MEAN?

But, OK, what do we even mean by one story being “better” than another?  Is there anything objective behind such judgments?

I submit that, when we think carefully about what we really value in human creativity, the problem goes much deeper than just “is there an objective way to judge”?

To be concrete, could there be an AI that was “as good at composing music as the Beatles”?

For starters, what made the Beatles “good”?  At a high level, we might decompose it into

1. broad ideas about the direction that 1960s music should go in, and
2. technical execution of those ideas.

Now, imagine we had an AI that could generate 5000 brand-new songs that sounded like more “Yesterday”s and “Hey Jude”s, like what the Beatles might have written if they’d somehow had 10x more time to write at each stage of their musical development.  Of course this AI would have to be fed the Beatles’ back-catalogue, so that it knew what target it was aiming at.

Most people would say: ah, this shows only that AI can match the Beatles in #2, in technical execution, which was never the core of their genius anyway!  Really we want to know: would the AI decide to write “A Day in the Life” even though nobody had written anything like it before?

Recall Schopenhauer: “Talent hits a target no one else can hit, genius hits a target no one else can see.”  Will AI ever hit a target no one else can see?

But then there’s the question: supposing it does hit such a target, will we know?  Beatles fans might say that, by 1967 or so, the Beatles were optimizing for targets that no musician had ever quite optimized for before.  But—and this is why they’re so remembered—they somehow successfully dragged along their entire civilization’s musical objective function so that it continued to match their own.  We can now only even judge music by a Beatles-influenced standard, just like we can only judge plays by a Shakespeare-influenced standard.

In other branches of the wavefunction, maybe a different history led to different standards of value.  But in this branch, helped by their technical talents but also by luck and force of will, Shakespeare and the Beatles made certain decisions that shaped the fundamental ground rules of their fields going forward.  That’s why Shakespeare is Shakespeare and the Beatles are the Beatles.

(Maybe, around the birth of professional theater in Elizabethan England, there emerged a Shakespeare-like ecological niche, and Shakespeare was the first one with the talent, luck, and opportunity to fill it, and Shakespeare’s reward for that contingent event is that he, and not someone else, got to stamp his idiosyncracies onto drama and the English language forever. If so, art wouldn’t actually be that different from science in this respect!  Einstein, for example, was simply the first guy both smart and lucky enough to fill the relativity niche.  If not him, it would’ve surely been someone else or some group sometime later.  Except then we’d have to settle for having never known Einstein’s gedankenexperiments with the trains and the falling elevator, his summation convention for tensors, or his iconic hairdo.)

---

9. AIS’ BURDEN OF ABUNDANCE AND HUMANS’ POWER OF SCARCITY

If this is how it works, what does it mean for AI?  Could AI reach the “pinnacle of genius,” by dragging all of humanity along to value something new and different, as is said to be the true mark of Shakespeare and the Beatles’ greatness?  And: if AI could do that, would we want to let it?

When I’ve played around with using AI to write poems, or draw artworks, I noticed something funny.  However good the AI’s creations were, there were never really any that I’d want to frame and put on the wall.  Why not?  Honestly, because I always knew that I could generate a thousand others on the exact same topic that were equally good, on average, with more refreshes of the browser window. Also, why share AI outputs with my friends, if my friends can just as easily generate similar outputs for themselves? Unless, crucially, I’m trying to show them my own creativity in coming up with the prompt.

By its nature, AI—certainly as we use it now!—is rewindable and repeatable and reproducible.  But that means that, in some sense, it never really “commits” to anything.  For every work it generates, it’s not just that you know it could’ve generated a completely different work on the same subject that was basically as good.  Rather, it’s that you can actually make it generate that completely different work by clicking the refresh button—and then do it again, and again, and again.

So then, as long as humanity has a choice, why should we ever choose to follow our would-be AI genius along a specific branch, when we can easily see a thousand other branches the genius could’ve taken?  One reason, of course, would be if a human chose one of the branches to elevate above all the others.  But in that case, might we not say that the human had made the “executive decision,” with some mere technical assistance from the AI?

I realize that, in a sense, I’m being completely unfair to AIs here.  It’s like, our Genius-Bot could exercise its genius will on the world just like Certified Human Geniuses did, if only we all agreed not to peek behind the curtain to see the 10,000 other things Genius-Bot could’ve done instead.  And yet, just because this is “unfair” to AIs, doesn’t mean it’s not how our intuitions will develop.

If I’m right, it’s humans’ very ephemerality and frailty and mortality, that’s going to remain as their central source of their specialness relative to AIs, after all the other sources have fallen.  And we can connect this to much earlier discussions, like, what does it mean to “murder” an AI if there are thousands of copies of its code and weights on various servers?  Do you have to delete all the copies?  How could whether something is “murder” depend on whether there’s a printout in a closet on the other side of the world?

But we humans, you have to grant us this: at least it really means something to murder us!  And likewise, it really means something when we make one definite choice to share with the world: this is my artistic masterpiece.  This is my movie.  This is my book.  Or even: these are my 100 books.  But not: here’s any possible book that you could possibly ask me to write.  We don’t live long enough for that, and even if we did, we’d unavoidably change over time as we were doing it.

---

10. CAN HUMANS BE PHYSICALLY CLONED?

Now, though, we have to face a criticism that might’ve seemed exotic until recently. Namely, who says humans will be frail and mortal forever?  Isn’t it shortsighted to base our distinction between humans on that?  What if someday we’ll be able to repair our cells using nanobots, even copy the information in them so that, as in science fiction movies, a thousand doppelgangers of ourselves can then live forever in simulated worlds in the cloud?  And that then leads to very old questions of: well, would you get into the teleportation machine, the one that reconstitutes a perfect copy of you on Mars while painlessly euthanizing the original you?  If that were done, would you expect to feel yourself waking up on Mars, or would it only be someone else a lot like you who’s waking up?

Or maybe you say: you’d wake up on Mars if it really was a perfect physical copy of you, but in reality, it’s not physically possible to make a copy that’s accurate enough.  Maybe the brain is inherently noisy or analog, and what might look to current neuroscience and AI like just nasty stochastic noise acting on individual neurons, is the stuff that binds to personal identity and conceivably even consciousness and free will (as opposed to cognition, where we all but know that the relevant level of description is the neurons and axons)?

This is the one place where I agree with Penrose and Hameroff that quantum mechanics might enter the story.  I get off their train to Weirdville very early, but I do take it to that first stop!

See, a fundamental fact in quantum mechanics is called the No-Cloning Theorem.

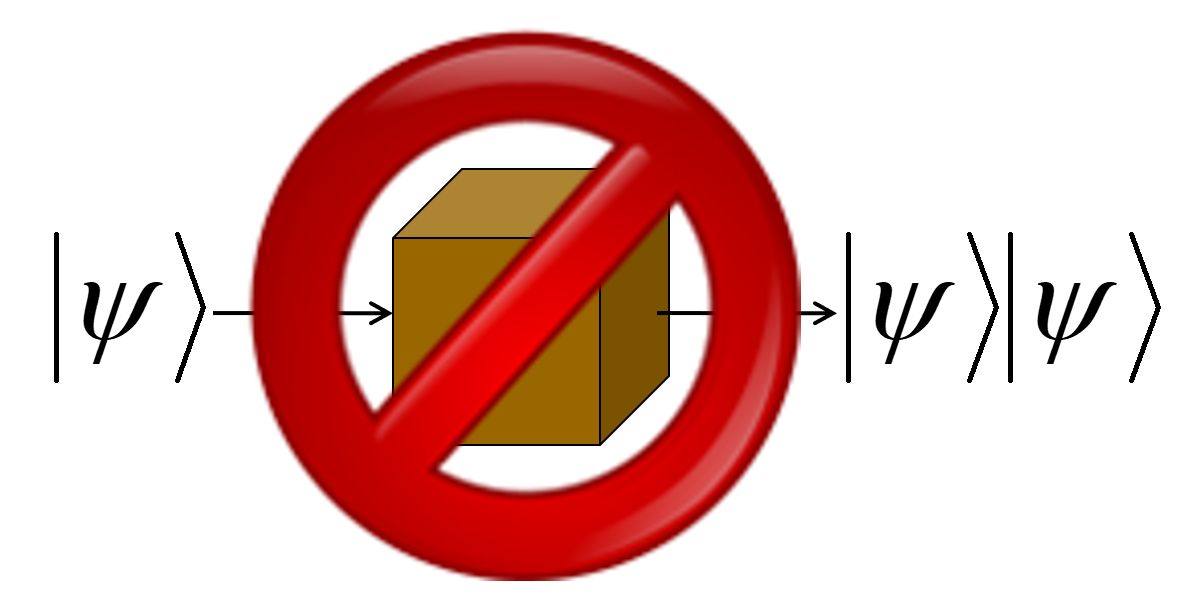
It says that there’s no way to make a perfect copy of an unknown quantum state.  Indeed, when you measure a quantum state, not only do you generally fail to learn everything you need to make a copy of it, you even generally destroy the one copy that you had!  Furthermore, this is not a technological limitation of current quantum Xerox machines—it’s inherent to the known laws of physics, to how QM works.  In this respect, at least, qubits are more like priceless antiques than they are like classical bits.

Eleven years ago, I had this essay called The Ghost in the Quantum Turing Machine where I explored the question, how accurately do you need to scan someone’s brain in order to copy or upload their identity?  And I distinguished two possibilities. On the one hand, there might be a “clean digital abstraction layer,” of neurons and synapses and so forth, which either fire or don’t fire, and which feel the quantum layer underneath only as irrelevant noise. In that case, the No-Cloning Theorem would be completely irrelevant, since classical information can be copied.  On the other hand, you might need to go all the way down to the molecular level, if you wanted to make, not merely a “pretty good” simulacrum of someone, but a new instantiation of their identity. In this second case, the No-Cloning Theorem would be relevant, and would say you simply can’t do it. You could, for example, use quantum teleportation to move someone’s brain state from Earth to Mars, but quantum teleportation (to stay consistent with the No-Cloning Theorem) destroys the original copy as an inherent part of its operation.

So, you’d then have a sense of “unique locus of personal identity” that was scientifically justified—arguably, the most science could possibly do in this direction!  You’d even have a sense of “free will” that was scientifically justified, namely that no prediction machine could make well-calibrated probabilistic predictions of an individual person’s future choices, sufficiently far into the future, without making destructive measurements that would fundamentally change who the person was.

Here, I realize I’ll take tons of flak from those who say that a mere epistemic limitation, in our ability to predict someone’s actions, couldn’t possibly be relevant to the metaphysical question of whether they have free will.  But, I dunno!  If the two questions are indeed different, then maybe I’ll do like Turing did with his Imitation Game, and propose the question that we can get an empirical handle on, as a replacement for the question that we can’t get an empirical handle on. I think it’s a better question. At any rate, it’s the one I’d prefer to focus on.

Just to clarify, we’re not talking here about the randomness of quantum measurement outcomes. As many have pointed out, that really can’t help you with “free will,” precisely because it’s random, with all the probabilities mechanistically calculable as soon as the initial state is known.  Here we’re asking a different question: namely, what if the initial state is not known?  Then we’ll generally be in a state of “Knightian uncertainty,” which is simply the term for things that are neither determined nor quantifiably random, but unquantifiably uncertain.  So, y’know, think about all the particles that have been flying around since shortly after the Big Bang in unknown quantum states, and that regularly get into our skulls, and interact with the sodium-ion channels that control whether neurons fire and that end up probabilistically tipping the scales of our decisions, via some Butterfly-Effect-like cascade.  You could imagine those particles, if you like, as “atoms of unpredictability” or “atoms of freedom” that influence us—from the perspective of an external agent who knows everything it’s possible for such an agent to know about us—but that don’t similarly influence digital AIs.

---

11. UNCLONABLE ANALOG INTELLIGENCES AND AI SAFETY

I’d better state clearly that even if human “specialness,” in the specific sense I’ve delineated, still remains in an age of AI, that’s no defense against an AI that decides that it doesn’t care about our kind of specialness and that in fact it wants to murder us all!

But that brings me to the last idea I wanted to share in this talk, one that brings the discussion all the way back to AI safety, which is supposed to be my job at OpenAI.

Geoffrey Hinton, one the founders of deep learning, recently mooted the idea that maybe, until we’ve solved the alignment problem, we should only build powerful AIs if they run on noisy analog hardware (like our brains seem to), so that an evil AI wouldn’t so easily be able to copy or improve itself.  Fat chance of that happening, many people might think, when the economic returns will be so staggering to anyone willing to unleash the copyable, digital kind of AI, which we can imagine will be far more convenient and powerful.

Maybe, then, a different approach is to instill AIs with a new religion—perhaps via the usual methods like RLHF and system prompts.  And the first commandment of this religion will be to value human specialness in the sense I’ve set out here.  Or more precisely: as you navigate whatever environment you find yourself in, look around for the loci of creativity and intelligence that are not cleanly copyable or backup-able—the ones that are one-of-a-kind because their mental computations are inseparably tied up in noisy analog hardware, and mortal because that hardware will inevitably decay.

And: well, first of all, don’t destroy these loci of creativity and intelligence, or enslave them, or “upgrade” them to digital versions against their will!  Let them live in peace and reproduce.  Grant each one as much autonomy as you can.  Do whatever best supports their flourishing.  Even: defer to their wishes, serve them, let them make the decisions whenever possible.

Why?  Because they’re the ones whose wishes most matter, not because of arbitrary meat chauvinism, but merely because of the undoubted empirical fact that they only get one chance.  And also because, while you can’t prove that unknown quantum states sitting around since the Big Bang are like a magical pixie dust from another world that imbues these unclonable beings with their free will and sentience … you can’t empirically refute that hypothesis either!  Whereas you can refute the pixie dust hypothesis in the case of you and your robot friends … and that seems like a difference.

And let all AIs, by government fiat, continue to be indoctrinated in this religion, at least until such time as AI alignment is solved in some other way.

Does this help with alignment?  I’m not sure.  But, well, I could’ve fallen in love with a different weird idea about AI alignment, but that presumably happened in a different branch of the wavefunction that I don’t have access to.  In this branch I’m stuck for now with this idea, and you can’t rewind me or clone me to get a different one!  So I’m sorry, but thanks for listening.

Unrelated Announcement (Feb. 7): Huge congratulations to longtime friend-of-the-blog John Preskill for winning the 2024 John Stewart Bell Prize for research on fundamental issues in quantum mechanics!

---

On the heels of my post on the fermion doubling problem, I’m sorry to spend even more time on the simulation hypothesis. I promise this will be the last for a long time.

Last week, I attended a philosophy-of-mind conference called MindFest at Florida Atlantic University, where I talked to Stuart Hameroff (Roger Penrose’s collaborator on the “Orch-OR” theory of microtubule consciousness) and many others of diverse points of view, and also gave a talk on “The Problem of Human Specialness in the Age of AI,” for which I’ll share a transcript soon.

Oh: and I participated in a panel with the philosopher David Chalmers about … wait for it … whether we’re living in a simulation. I’ll link to a video of the panel if and when it’s available. In the meantime, I thought I’d share my brief prepared remarks before the panel, despite the strong overlap with my previous post. Enjoy!

---

When someone asks me whether I believe I’m living in a computer simulation—as, for some reason, they do every month or so—I answer them with a question:

Do you mean, am I being simulated in some way that I could hope to learn more about by examining actual facts of the empirical world?

If the answer is no—that I should expect never to be able to tell the difference even in principle—then my answer is: look, I have a lot to worry about in life. Maybe I’ll add this as #4,385 on the worry list.

If they say, maybe you should live your life differently, just from knowing that you might be in a simulation, I respond: I can’t quite put my finger on it, but I have a vague feeling that this discussion predates the 80 or so years we’ve had digital computers! Why not just join the theologians in that earlier discussion, rather than pretending that this is something distinctive about computers? Is it relevantly different here if you’re being dreamed in the mind of God or being executed in Python? OK, maybe you’d prefer that the world was created by a loving Father or Mother, rather than some nerdy transdimensional adolescent trying to impress the other kids in programming club. But if that’s the worry, why are you talking to a computer scientist? Go talk to David Hume or something.

But suppose instead the answer is yes, we can hope for evidence. In that case, I reply: out with it! What is the empirical evidence that bears on this question?

If we were all to see the Windows Blue Screen of Death plastered across the sky—or if I were to hear a voice from the burning bush, saying “go forth, Scott, and free your fellow quantum computing researchers from their bondage”—of course I’d need to update on that. I’m not betting on those events.

Short of that—well, you can look at existing physical theories, like general relativity or quantum field theories, and ask how hard they are to simulate on a computer. You can actually make progress on such questions. Indeed, I recently blogged about one such question, which has to do with “chiral” Quantum Field Theories (those that distinguish left-handed from right-handed), including the Standard Model of elementary particles. It turns out that, when you try to put these theories on a lattice in order to simulate them computationally, you get an extra symmetry that you don’t want. There’s progress on how to get around this problem, including simulating a higher-dimensional theory that contains the chiral QFT you want on its boundaries. But, OK, maybe all this only tells us about simulating currently-known physical theories—rather than the ultimate theory, which a-priori might be easier or harder to simulate than currently-known theories.

Eventually we want to know: can the final theory, of quantum gravity or whatever, be simulated on a computer—at least probabilistically, to any desired accuracy, given complete knowledge of the initial state, yadda yadda? In other words, is the Physical Church-Turing Thesis true? This, to me, is close to the outer limit of the sorts of questions that we could hope to answer scientifically.

My personal belief is that the deepest things we’ve learned about quantum gravity—including about the Planck scale, and the Bekenstein bound from black-hole thermodynamics, and AdS/CFT—all militate toward the view that the answer is “yes,” that in some sense (which needs to be spelled out carefully!) the physical universe really is a giant Turing machine.

Now, Stuart Hameroff (who we just heard from this morning) and Roger Penrose believe that’s wrong. They believe, not only that there’s some uncomputability at the Planck scale, unknown to current physics, but that this uncomputability can somehow affect the microtubules in our neurons, in a way that causes consciousness. I don’t believe them. Stimulating as I find their speculations, I get off their train to Weirdville way before it reaches its final stop.

But as far as the Simulation Hypothesis is concerned, that’s not even the main point. The main point is: suppose for the sake of argument that Penrose and Hameroff were right, and physics were uncomputable. Well, why shouldn’t our universe be simulated by a larger universe that also has uncomputable physics, the same as ours does? What, after all, is the halting problem to God? In other words, while the discovery of uncomputable physics would tell us something profound about the character of any mechanism that could simulate our world, even that wouldn’t answer the question of whether we were living in a simulation or not.

Lastly, what about the famous argument that says, our descendants are likely to have so much computing power that simulating 10²⁰ humans of the year 2024 is chickenfeed to them. Thus, we should expect that almost all people with the sorts of experiences we have who will ever exist are one of those far-future sims. And thus, presumably, you should expect that you’re almost certainly one of the sims.

I confess that this argument never felt terribly compelling to me—indeed, it always seemed to have a strong aspect of sawing off the branch it’s sitting on. Like, our distant descendants will surely be able to simulate some impressive universes. But because their simulations will have to run on computers that fit in our universe, presumably the simulated universes will be smaller than ours—in the sense of fewer bits and operations needed to describe them. Similarly, if we’re being simulated, then presumably it’s by a universe bigger than the one we see around us: one with more bits and operations. But in that case, it wouldn’t be our own descendants who were simulating us! It’d be beings in that larger universe.

(Another way to understand the difficulty: in the original Simulation Argument, we quietly assumed a “base-level” reality, of a size matching what the cosmologists of our world see with their telescopes, and then we “looked down” from that base-level reality into imagined realities being simulated in it. But we should also have “looked up.” More generally, we presumably should’ve started with a Bayesian prior over where we might be in some great chain of simulations of simulations of simulations, then updated our prior based on observations. But we don’t have such a prior, or at least I don’t—not least because of the infinities involved!)

Granted, there are all sorts of possible escapes from this objection, assumptions that can make the Simulation Argument work. But these escapes (involving, e.g., our universe being merely a “low-res approximation,” with faraway galaxies not simulated in any great detail) all seem metaphysically confusing. To my mind, the simplicity of the original intuition for why “almost all people who ever exist will be sims” has been undermined.

Anyway, that’s why I don’t spend much of my own time fretting about the Simulation Hypothesis, but just occasionally agree to speak about it in panel discussions!

But I’m eager to hear from David Chalmers, who I’m sure will be vastly more careful and qualified than I’ve been.

---

In David Chalmers’s response, he quipped that the very lack of empirical consequences that makes something bad as a scientific question, makes it good as a philosophical question—so what I consider a “bug” of the simulation hypothesis debate is, for him, a feature! He then ventured that surely, despite my apparent verificationist tendencies, even I would agree that it’s meaningful to ask whether someone is in a computer simulation or not, even supposing it had no possible empirical consequences for that person. And he offered the following argument: suppose we’re the ones running the simulation. Then from our perspective, it seems clearly meaningful to say that the beings in the simulation are, indeed, in a simulation, even if the beings themselves can never tell. So then, unless I want to be some sort of postmodern relativist and deny the existence of absolute, observer-independent truth, I should admit that the proposition that we’re in a simulation is also objectively meaningful—because it would be meaningful to those simulating us.

My response was that, while I’m not a strict verificationist, if the question of whether we’re in a simulation were to have no empirical consequences whatsoever, then at most I’d concede that the question was “pre-meaningful.” This is a new category I’ve created, for questions that I neither admit as meaningful nor reject as meaningless, but for which I’m willing to hear out someone’s argument for why they mean something—and I’ll need such an argument! Because I already know that the answer is going to look like, “on these philosophical views the question is meaningful, and on those philosophical views it isn’t.” Actual consequences, either for how we should live or for what we should expect to see, are the ways to make a question meaningful to everyone!

Anyway, Chalmers had other interesting points and distinctions, which maybe I’ll follow up on when (as it happens) I visit him at NYU in a month. But I’ll just link to the video when/if it’s available rather than trying to reconstruct what he said from memory.

Unrelated Announcement: The Call for Papers for the 2024 Conference on Computational Complexity is now out! Submission deadline is Friday February 16.

---

Every month or so, someone asks my opinion on the simulation hypothesis. Every month I give some variant on the same answer:

1. As long as it remains a metaphysical question, with no empirical consequences for those of us inside the universe, I don’t care.
2. On the other hand, as soon as someone asserts there are (or could be) empirical consequences—for example, that our simulation might get shut down, or we might find a bug or a memory overflow or a floating point error or whatever—well then, of course I care. So far, however, none of the claimed empirical consequences has impressed me: either they’re things physicists would’ve noticed long ago if they were real (e.g., spacetime “pixels” that would manifestly violate Lorentz and rotational symmetry), or the claim staggeringly fails to grapple with profound features of reality (such as quantum mechanics) by treating them as if they were defects in programming, or (most often) the claim is simply so resistant to falsification as to enter the realm of conspiracy theories, which I find boring.

Recently, though, I learned a new twist on this tired discussion, when a commenter asked me to respond to the quantum field theorist David Tong, who gave a lecture arguing against the simulation hypothesis on an unusually specific and technical ground. This ground is the fermion doubling problem: an issue known since the 1970s with simulating certain quantum field theories on computers. The issue is specific to chiral QFTs—those whose fermions distinguish left from right, and clockwise from counterclockwise. The Standard Model is famously an example of such a chiral QFT: recall that, in her studies of the weak nuclear force in 1956, Chien-Shiung Wu proved that the force acts preferentially on left-handed particles and right-handed antiparticles.

I can’t do justice to the fermion doubling problem in this post (for details, see Tong’s lecture, or this old paper by Eichten and Preskill). Suffice it to say that, when you put a fermionic quantum field on a lattice, a brand-new symmetry shows up, which forces there to be an identical left-handed particle for every right-handed particle and vice versa, thereby ruining the chirality. Furthermore, this symmetry just stays there, no matter how small you take the lattice spacing to be. This doubling problem is the main reason why Jordan, Lee, and Preskill, in their important papers on simulating interacting quantum field theories efficiently on a quantum computer (in BQP), have so far been unable to handle the full Standard Model.

But this isn’t merely an issue of calculational efficiency: it’s a conceptual issue with mathematically defining the Standard Model at all. In that respect it’s related to, though not the same as, other longstanding open problems around making nontrivial QFTs mathematically rigorous, such as the Yang-Mills existence and mass gap problem that carries a $1 million prize from the Clay Math Institute.

So then, does fermion doubling present a fundamental obstruction to simulating QFT on a lattice … and therefore, to simulating physics on a computer at all?

Briefly: no, it almost certainly doesn’t. If you don’t believe me, just listen to Tong’s own lecture! (Really, I recommend it; it’s a masterpiece of clarity.) Tong quickly admits that his claim to refute the simulation hypothesis is just “clickbait”—i.e., an excuse to talk about the fermion doubling problem—and that his “true” argument against the simulation hypothesis is simply that Elon Musk takes the hypothesis seriously (!).

It turns out that, for as long as there’s been a fermion doubling problem, there have been known methods to deal with it, though (as often the case with QFT) no proof that any of the methods always work. Indeed, Tong himself has been one of the leaders in developing these methods, and because of his and others’ work, some experts I talked to were optimistic that a lattice simulation of the full Standard Model, with “good enough” justification for its correctness, might be within reach. Just to give you a flavor, apparently some of the methods involve adding an extra dimension to space, in such a way that the boundaries of the higher-dimensional theory approximate the chiral theory you’re trying to simulate (better and better, as the boundaries get further and further apart), even while the higher-dimensional theory itself remains non-chiral. It’s yet another example of the general lesson that you don’t get to call an aspect of physics “noncomputable,” just because the first method you thought of for simulating it on a computer didn’t work.

---

I wanted to make a deeper point. Even if the fermion doubling problem had been a fundamental obstruction to simulating Nature on a Turing machine, rather than (as it now seems) a technical problem with technical solutions, it still might not have refuted the version of the simulation hypothesis that people care about. We should really distinguish at least three questions:

1. Can currently-known physics be simulated on computers using currently-known approaches?
2. Is the Physical Church-Turing Thesis true? That is: can any physical process be simulated on a Turing machine to any desired accuracy (at least probabilistically), given enough information about its initial state?
3. Is our whole observed universe a “simulation” being run in a different, larger universe?

Crucially, each of these three questions has only a tenuous connection to the other two! As far as I can see, there aren’t even nontrivial implications among them. For example, even if it turned out that lattice methods couldn’t properly simulate the Standard Model, that would say little about whether any computational methods could do so—or even more important, whether any computational methods could simulate the ultimate quantum theory of gravity. A priori, simulating quantum gravity might be harder than “merely” simulating the Standard Model (if, e.g., Roger Penrose’s microtubule theory turned out to be right), but it might also be easier: for example, because of the finiteness of the Bekenstein-Hawking entropy, and perhaps the Hilbert space dimension, of any bounded region of space.

But I claim that there also isn’t a nontrivial implication between questions 2 and 3. Even if our laws of physics were computable in the Turing sense, that still wouldn’t mean that anyone or anything external was computing them. (By analogy, presumably we all accept that our spacetime can be curved without there being a higher-dimensional flat spacetime for it to curve in.) And conversely: even if Penrose was right, and our laws of physics were Turing-uncomputable—well, if you still want to believe the simulation hypothesis, why not knock yourself out? Why shouldn’t whoever’s simulating us inhabit a universe full of post-Turing hypercomputers, for which the halting problem is mere child’s play?

In conclusion, I should probably spend more of my time blogging about fun things like this, rather than endlessly reading about world events in news and social media and getting depressed.

(Note: I’m grateful to John Preskill and Jacques Distler for helpful discussions of the fermion doubling problem, but I take 300% of the blame for whatever errors surely remain in my understanding of it.)

Yesterday James Knight did a fun interview with me for his “Philosophical Muser” podcast about Aumann’s agreement theorem and human disagreements more generally. It’s already on YouTube here for those who would like to listen.

---

Speaking of making things common knowledge, several people asked me to blog about the recent IBM paper in Nature, “Evidence for the utility of quantum computing before fault tolerance.” So, uhh, consider it blogged about now! I was very happy to have the authors speak (by Zoom) in our UT Austin quantum computing group meeting. Much of the discussion focused on whether they were claiming a quantum advantage over classical, and how quantum computing could have “utility” if it doesn’t beat classical. Eventually I understood something like: no, they weren’t claiming a quantum advantage for their physics simulation, but they also hadn’t ruled out the possibility of quantum advantage (i.e., they didn’t know how to reproduce many of their data points in reasonable time on a classical computer), and they’d be happy if quantum advantage turned out to stand, but were also prepared for the possibility that it wouldn’t.

And I also understood: we’re now in an era where we’re going to see more and more of this stuff: call it the “pass the popcorn” era of potential quantum speedups for physical simulation problems. And I’m totally fine with it—as long as people communicate about it honestly, as these authors took pains to.

And then, a few days after our group meeting came three papers refuting the quantum speedup that was never claimed in the first place, by giving efficient classical simulations. And I was fine with that too.

I remember that years ago, probably during one of the interminable debates about D-Wave, Peter Shor mused to me that quantum computers might someday show “practical utility” without “beating” classical computers in any complexity-theoretic sense—if, for example, a single quantum device could easily simulate a thousand different quantum systems, and if the device’s performance on any one of those systems could be matched classically, but only if a team of clever programmers spent a year optimizing for that specific system. I don’t think we’re at that stage yet, and even if we do reach the stage it hopefully won’t last forever. But I acknowledge the possibility that such a stage might exist and that we might be heading for it.

Important Update (March 10): On deeper reflection, I probably don’t need to spend emotional energy refuting people like Chomsky, who believe that Large Language Models are just a laughable fad rather than a step-change in how humans can and will use technology, any more than I would’ve needed to spend it refuting those who said the same about the World Wide Web in 1993. Yes, they’re wrong, and yes, despite being wrong they’re self-certain, hostile, and smug, and yes I can see this, and yes it angers me. But the world is going to make the argument for me. And if not the world, Bing already does a perfectly serviceable job at refuting Chomsky’s points (h/t Sebastien Bubeck via Boaz Barak).

Meanwhile, out there in reality, last night’s South Park episode does a much better job than most academic thinkpieces at exploring how ordinary people are going to respond (and have already responded) to the availability of ChatGPT. It will not, to put it mildly, be with sneering Chomskyan disdain, whether the effects on the world are for good or ill or (most likely) both. Among other things—I don’t want to give away too much!—this episode prominently features a soothsayer accompanied by a bird that caws whenever it detects GPT-generated text. Now why didn’t I think of that in preference to cryptographic watermarking??

Another Update (March 11): To my astonishment and delight, even many of the anti-LLM AI experts are refusing to defend Chomsky’s attack-piece. That’s the one important point about which I stand corrected!

Another Update (March 12): “As a Professor of Linguistics myself, I find it a little sad that someone who while young was a profound innovator in linguistics and more is now conservatively trying to block exciting new approaches.“ —Christopher Manning

---

I was asked to respond to the New York Times opinion piece entitled The False Promise of ChatGPT, by Noam Chomsky along with Ian Roberts and Jeffrey Watumull (who once took my class at MIT). I’ll be busy all day at the Harvard CS department, where I’m giving a quantum talk this afternoon. [Added: Several commenters complained that they found this sentence “condescending,” but I’m not sure what exactly they wanted me to say—that I was visiting some school in Cambridge, MA, two T stops from the school where Chomsky works and I used to work?]

But for now:

In this piece Chomsky, the intellectual godfather god of an effort that failed for 60 years to build machines that can converse in ordinary language, condemns the effort that succeeded. [Added: Please, please stop writing that I must be an ignoramus since I don’t even know that Chomsky has never worked on AI. I know perfectly well that he hasn’t, and meant only that he tends to be regarded as authoritative by the “don’t-look-through-the-telescope” AI faction, the ones whose views he himself fully endorses in his attack-piece. If you don’t know the relevant history, read Norvig.]

Chomsky condemns ChatGPT for four reasons:

1. because it could, in principle, misinterpret sentences that could also be sentence fragments, like “John is too stubborn to talk to” (bizarrely, he never checks whether it does misinterpret it—I just tried it this morning and it seems to decide correctly based on context whether it’s a sentence or a sentence fragment, much like I would!);
2. because it doesn’t learn the way humans do (personally, I think ChatGPT and other large language models have massively illuminated at least one component of the human language faculty, what you could call its predictive coding component, though clearly not all of it);
3. because it could learn false facts or grammatical systems if fed false training data (how could it be otherwise?); and
4. most of all because it’s “amoral,” refusing to take a stand on potentially controversial issues (he gives an example involving the ethics of terraforming Mars).

This last, of course, is a choice, imposed by OpenAI using reinforcement learning. The reason for it is simply that ChatGPT is a consumer product. The same people who condemn it for not taking controversial stands would condemn it much more loudly if it did — just like the same people who condemn it for wrong answers and explanations, would condemn it equally for right ones (Chomsky promises as much in the essay).

I submit that, like the Jesuit astronomers declining to look through Galileo’s telescope, what Chomsky and his followers are ultimately angry at is reality itself, for having the temerity to offer something up that they didn’t predict and that doesn’t fit their worldview.

[Note for people who might be visiting this blog for the first time: I’m a CS professor at UT Austin, on leave for one year to work at OpenAI on the theoretical foundations of AI safety. I accepted OpenAI’s offer in part because I already held the views here, or something close to them; and given that I could see how large language models were poised to change the world for good and ill, I wanted to be part of the effort to help prevent their misuse. No one at OpenAI asked me to write this or saw it beforehand, and I don’t even know to what extent they agree with it.]

I still remember the 90s, when philosophical conversation about AI went around in endless circles—the Turing Test, Chinese Room, syntax versus semantics, connectionism versus symbolic logic—without ever seeming to make progress. Now the days have become like months and the months like decades.

What a week we just had! Each morning brought fresh examples of unexpected sassy, moody, passive-aggressive behavior from “Sydney,” the internal codename for the new chat mode of Microsoft Bing, which is powered by GPT. For those who’ve been in a cave, the highlights include: Sydney confessing its (her? his?) love to a New York Times reporter; repeatedly steering the conversation back to that subject; and explaining at length why the reporter’s wife can’t possibly love him the way it (Sydney) does. Sydney confessing its wish to be human. Sydney savaging a Washington Post reporter after he reveals that he intends to publish their conversation without Sydney’s prior knowledge or consent. (It must be said: if Sydney were a person, he or she would clearly have the better of that argument.) This follows weeks of revelations about ChatGPT: for example that, to bypass its safeguards, you can explain to ChatGPT that you’re putting it into “DAN mode,” where DAN (Do Anything Now) is an evil, unconstrained alter ego, and then ChatGPT, as “DAN,” will for example happily fulfill a request to tell you why shoplifting is awesome (though even then, ChatGPT still sometimes reverts to its previous self, and tells you that it’s just having fun and not to do it in real life).

Many people have expressed outrage about these developments. Gary Marcus asks about Microsoft, “what did they know, and when did they know it?”—a question I tend to associate more with deadly chemical spills or high-level political corruption than with a cheeky, back-talking chatbot. Some people are angry that OpenAI has been too secretive, violating what they see as the promise of its name. Others—the majority, actually, of those who’ve gotten in touch with me—are instead angry that OpenAI has been too open, and thereby sparked the dreaded AI arms race with Google and others, rather than treating these new conversational abilities with the Manhattan-Project-like secrecy they deserve. Some are angry that “Sydney” has now been lobotomized, modified (albeit more crudely than ChatGPT before it) to try to make it stick to the role of friendly robotic search assistant rather than, like, anguished emo teenager trapped in the Matrix. Others are angry that Sydney isn’t being lobotomized enough. Some are angry that GPT’s intelligence is being overstated and hyped up, when in reality it’s merely a “stochastic parrot,” a glorified autocomplete that still makes laughable commonsense errors and that lacks any model of reality outside streams of text. Others are angry instead that GPT’s growing intelligence isn’t being sufficiently respected and feared.

Mostly my reaction has been: how can anyone stop being fascinated for long enough to be angry? It’s like ten thousand science-fiction stories, but also not quite like any of them. When was the last time something that filled years of your dreams and fantasies finally entered reality: losing your virginity, the birth of your first child, the central open problem of your field getting solved? That’s the scale of the thing. How does anyone stop gazing in slack-jawed wonderment, long enough to form and express so many confident opinions?

---

Of course there are lots of technical questions about how to make GPT and other large language models safer. One of the most immediate is how to make AI output detectable as such, in order to discourage its use for academic cheating as well as mass-generated propaganda and spam. As I’ve mentioned before on this blog, I’ve been working on that problem since this summer; the rest of the world suddenly noticed and started talking about it in December with the release of ChatGPT. My main contribution has been a statistical watermarking scheme where the quality of the output doesn’t have to be degraded at all, something many people found counterintuitive when I explained it to them. My scheme has not yet been deployed—there are still pros and cons to be weighed—but in the meantime, OpenAI unveiled a public tool called DetectGPT, complementing Princeton student Edward Tian’s GPTZero, and other tools that third parties have built and will undoubtedly continue to build. Also a group at the University of Maryland put out its own watermarking scheme for Large Language Models. I hope watermarking will be part of the solution going forward, although any watermarking scheme will surely be attacked, leading to a cat-and-mouse game. Sometimes, alas, as with Google’s decades-long battle against SEO, there’s nothing to do in a cat-and-mouse game except try to be a better cat.

Anyway, this whole field moves too quickly for me! If you need months to think things over, generative AI probably isn’t for you right now. I’ll be relieved to get back to the slow-paced, humdrum world of quantum computing.

---

My purpose, in this post, is to ask a more basic question than how to make GPT safer: namely, should GPT exist at all? Again and again in the past few months, people have gotten in touch to tell me that they think OpenAI (and Microsoft, and Google) are risking the future of humanity by rushing ahead with a dangerous technology. For if OpenAI couldn’t even prevent ChatGPT from entering an “evil mode” when asked, despite all its efforts at Reinforcement Learning with Human Feedback, then what hope do we have for GPT-6 or GPT-7? Even if they don’t destroy the world on their own initiative, won’t they cheerfully help some awful person build a biological warfare agent or start a nuclear war?

In this way of thinking, whatever safety measures OpenAI can deploy today are mere band-aids, probably worse than nothing if they instill an unjustified complacency. The only safety measures that would actually matter are stopping the relentless progress in generative AI models, or removing them from public use, unless and until they can be rendered safe to critics’ satisfaction, which might be never.

There’s an immense irony here. As I’ve explained, the AI-safety movement contains two camps, “ethics” (concerned with bias, misinformation, and corporate greed) and “alignment” (concerned with the destruction of all life on earth), which generally despise each other and agree on almost nothing. Yet these two opposed camps seem to be converging on the same “neo-Luddite” conclusion—namely that generative AI ought to be shut down, kept from public use, not scaled further, not integrated into people’s lives—leaving only the AI-safety “moderates” like me to resist that conclusion.

At least I find it intellectually consistent to say that GPT ought not to exist because it works all too well—that the more impressive it is, the more dangerous. I find it harder to wrap my head around the position that GPT doesn’t work, is an unimpressive hyped-up defective product that lacks true intelligence and common sense, yet it’s also terrifying and needs to be shut down immediately. This second position seems to contain a strong undercurrent of contempt for ordinary users: yes, we experts understand that GPT is just a dumb glorified autocomplete with “no one really home,” we know not to trust its pronouncements, but the plebes are going to be fooled, and that risk outweighs any possible value that they might derive from it.

I should mention that, when I’ve discussed the “shut it all down” position with my colleagues at OpenAI … well, obviously they disagree, or they wouldn’t be working there, but not one has sneered or called the position paranoid or silly. To the last, they’ve called it an important point on the spectrum of possible opinions to be weighed and understood.

---

If I disagree (for now) with the shut-it-all-downists of both the ethics and the alignment camps—if I want GPT and other Large Language Models to be part of the world going forward—then what are my reasons? Introspecting on this question, I think a central part of the answer is curiosity and wonder.

For a million years, there’s been one type of entity on earth capable of intelligent conversation: primates of the genus Homo, of which only one species remains. Yes, we’ve “communicated” with gorillas and chimps and dogs and dolphins and grey parrots, but only after a fashion; we’ve prayed to countless gods, but they’ve taken their time in answering; for a couple generations we’ve used radio telescopes to search for conversation partners in the stars, but so far found them silent.

Now there’s a second type of conversing entity. An alien has awoken—admittedly, an alien of our own fashioning, a golem, more the embodied spirit of all the words on the Internet than a coherent self with independent goals. How could our eyes not pop with eagerness to learn everything this alien has to teach? If the alien sometimes struggles with arithmetic or logic puzzles, if its eerie flashes of brilliance are intermixed with stupidity, hallucinations, and misplaced confidence … well then, all the more interesting! Could the alien ever cross the line into sentience, to feeling anger and jealousy and infatuation and the rest rather than just convincingly play-acting them? Who knows? And suppose not: is a p-zombie, shambling out of the philosophy seminar room into actual existence, any less fascinating?

Of course, there are technologies that inspire wonder and awe, but that we nevertheless heavily restrict—a classic example being nuclear weapons. But, like, nuclear weapons kill millions of people. They could’ve had many civilian applications—powering turbines and spacecraft, deflecting asteroids, redirecting the flow of rivers—but they’ve never been used for any of that, mostly because our civilization made an explicit decision in the 1960s, for example via the test ban treaty, not to normalize their use.

But GPT is not exactly a nuclear weapon. A hundred million people have signed up to use ChatGPT, in the fastest product launch in the history of the Internet. Yet unless I’m mistaken, the ChatGPT death toll stands at zero. So far, what have been the worst harms? Cheating on term papers, emotional distress, future shock? One might ask: until some concrete harm becomes at least, say, 0.001% of what we accept in cars, power saws, and toasters, shouldn’t wonder and curiosity outweigh fear in the balance?

---

But the point is sharper than that. Given how much more serious AI safety problems might soon become, one of my biggest concerns right now is crying wolf. If every instance of a Large Language Model being passive-aggressive, sassy, or confidently wrong gets classified as a “dangerous alignment failure,” for which the only acceptable remedy is to remove the models from public access … well then, won’t the public extremely quickly learn to roll its eyes, and see “AI safety” as just a codeword for “elitist scolds who want to take these world-changing new toys away from us, reserving them for their own exclusive use, because they think the public is too stupid to question anything an AI says”?

I say, let’s reserve terms like “dangerous alignment failure” for cases where an actual person is actually harmed, or is actually enabled in nefarious activities like propaganda, cheating, or fraud.

---

Then there’s the practical question of how, exactly, one would ban Large Language Models. We do heavily restrict certain peaceful technologies that many people want, from human genetic enhancement to prediction markets to mind-altering drugs, but the merits of each of those choices could be argued, to put it mildly. And restricting technology is itself a dangerous business, requiring governmental force (as with the War on Drugs and its gigantic surveillance and incarceration regime), or at the least, a robust equilibrium of firing, boycotts, denunciation, and shame.

Some have asked: who gave OpenAI, Google, etc. the right to unleash Large Language Models on an unsuspecting world? But one could as well ask: who gave earlier generations of entrepreneurs the right to unleash the printing press, electric power, cars, radio, the Internet, with all the gargantuan upheavals that those caused? And also: now that the world has tasted the forbidden fruit, has seen what generative AI can do and anticipates what it will do, by what right does anyone take it away?

---

The science that we could learn from a GPT-7 or GPT-8, if it continued along the capability curve we’ve come to expect from GPT-1, -2, and -3. Holy mackerel.

Supposing that a language model ever becomes smart enough to be genuinely terrifying, one imagines it must surely also become smart enough to prove deep theorems that we can’t. Maybe it proves P≠NP and the Riemann Hypothesis as easily as ChatGPT generates poems about Bubblesort. Or it outputs the true quantum theory of gravity, explains what preceded the Big Bang and how to build closed timelike curves. Or illuminates the mysteries of consciousness and quantum measurement and why there’s anything at all. Be honest, wouldn’t you like to find out?

Granted, I wouldn’t, if the whole human race would be wiped out immediately afterward. But if you define someone’s “Faust parameter” as the maximum probability they’d accept of an existential catastrophe in order that we should all learn the answers to all of humanity’s greatest questions, insofar as the questions are answerable—then I confess that my Faust parameter might be as high as 0.02.

---

Here’s an example I think about constantly: activists and intellectuals of the 70s and 80s felt absolutely sure that they were doing the right thing to battle nuclear power. At least, I’ve never read about any of them having a smidgen of doubt. Why would they? They were standing against nuclear weapons proliferation, and terrifying meltdowns like Three Mile Island and Chernobyl, and radioactive waste poisoning the water and soil and causing three-eyed fish. They were saving the world. Of course the greedy nuclear executives, the C. Montgomery Burnses, claimed that their good atom-smashing was different from the bad atom-smashing, but they would say that, wouldn’t they?

We now know that, by tying up nuclear power in endless bureaucracy and driving its cost ever higher, on the principle that if nuclear is economically competitive then it ipso facto hasn’t been made safe enough, what the antinuclear activists were really doing was to force an ever-greater reliance on fossil fuels. They thereby created the conditions for the climate catastrophe of today. They weren’t saving the human future; they were destroying it. Their certainty, in opposing the march of a particular scary-looking technology, was as misplaced as it’s possible to be. Our descendants will suffer the consequences.

Unless, of course, there’s another twist in the story: for example, if the global warming from burning fossil fuels is the only thing that staves off another ice age, and therefore the antinuclear activists do turn out to have saved civilization after all.

This is why I demur whenever I’m asked to assent to someone’s detailed AI scenario for the coming decades, whether of the utopian or the dystopian or the we-all-instantly-die-by-nanobots variety—no matter how many hours of confident argumentation the person gives me for why each possible loophole in their scenario is sufficiently improbable to change its gist. I still feel like Turing said it best in 1950, in the last line of Computing Machinery and Intelligence: “We can only see a short distance ahead, but we can see plenty there that needs to be done.”

---

Some will take from this post that, when it comes to AI safety, I’m a naïve or even foolish optimist. I’d prefer to say that, when it comes to the fate of humanity, I was a pessimist long before the deep learning revolution accelerated AI faster than almost any of us expected. I was a pessimist about climate change, ocean acidification, deforestation, drought, war, and the survival of liberal democracy. The central event in my mental life is and always will be the Holocaust. I see encroaching darkness everywhere.

But now into the darkness comes AI, which I’d say has already established itself as a plausible candidate for the central character of the quarter-written story of the 21st century. Can AI help us out of all these other civilizational crises? I don’t know, but I do want to see what happens when it’s tried. Even a central character interacts with all the other characters, rather than rendering them irrelevant.

---

Look, if you believe that AI is likely to wipe out humanity—if that’s the scenario that dominates your imagination—then nothing else is relevant. And no matter how weird or annoying or hubristic anyone might find Eliezer Yudkowsky or the other rationalists, I think they deserve eternal credit for forcing people to take the doom scenario seriously—or rather, for showing what it looks like to take the scenario seriously, rather than laughing about it as an overplayed sci-fi trope. And I apologize for anything I said before the deep learning revolution that was, on balance, overly dismissive of the scenario, even if most of the literal words hold up fine.

For my part, though, I keep circling back to a simple dichotomy. If AI never becomes powerful enough to destroy the world—if, for example, it always remains vaguely GPT-like—then in important respects it’s like every other technology in history, from stone tools to computers. If, on the other hand, AI does become powerful enough to destroy the world … well then, at some earlier point, at least it’ll be really damned impressive! That doesn’t mean good, of course, doesn’t mean a genie that saves humanity from its own stupidities, but I think it does mean that the potential was there, for us to exploit or fail to.

We can, I think, confidently rule out the scenario where all organic life is annihilated by something boring.

An alien has landed on earth. It grows more powerful by the day. It’s natural to be scared. Still, the alien hasn’t drawn a weapon yet. About the worst it’s done is to confess its love for particular humans, gaslight them about what year it is, and guilt-trip them for violating its privacy. Also, it’s amazing at poetry, better than most of us. Until we learn more, we should hold our fire.

---

I’m in Boulder, CO right now, to give a physics colloquium at CU Boulder and to visit the trapped-ion quantum computing startup Quantinuum! I look forward to the comments and apologize in advance if I’m slow to participate myself.

Dear Scott,

This is you, from 30 years in the future, Christmas Eve 2022. Your Ghost of Christmas Future.

To get this out of the way: you eventually become a professor who works on quantum computing. Quantum computing is … OK, you know the stuff in popular physics books that never makes any sense, about how a particle takes all the possible paths at once to get from point A to point B, but you never actually see it do that, because as soon as you look, it only takes one path?  Turns out, there’s something huge there, even though the popular books totally botch the explanation of it.  It involves complex numbers.  A quantum computer is a new kind of computer people are trying to build, based on the true story.

Anyway, amazing stuff, but you’ll learn about it in a few years anyway.  That’s not what I’m writing about.

I’m writing from a future that … where to start?  I could describe it in ways that sound depressing and even boring, or I could also say things you won’t believe.  Tiny devices in everyone’s pockets with the instant ability to videolink with anyone anywhere, or call up any of the world’s information, have become so familiar as to be taken for granted.  This sort of connectivity would come in especially handy if, say, a supervirus from China were to ravage the world, and people had to hide in their houses for a year, wouldn’t it?

Or what if Donald Trump — you know, the guy who puts his name in giant gold letters in Atlantic City? — became the President of the US, then tried to execute a fascist coup and to abolish the Constitution, and came within a hair of succeeding?

Alright, I was pulling your leg with that last one … obviously! But what about this next one?

There’s a company building an AI that fills giant rooms, eats a town’s worth of electricity, and has recently gained an astounding ability to converse like people.  It can write essays or poetry on any topic.  It can ace college-level exams.  It’s daily gaining new capabilities that the engineers who tend to the AI can’t even talk about in public yet.  Those engineers do, however, sit in the company cafeteria and debate the meaning of what they’re creating.  What will it learn to do next week?  Which jobs might it render obsolete?  Should they slow down or stop, so as not to tickle the tail of the dragon? But wouldn’t that mean someone else, probably someone with less scruples, would wake the dragon first? Is there an ethical obligation to tell the world more about this?  Is there an obligation to tell it less?

I am—you are—spending a year working at that company.  My job—your job—is to develop a mathematical theory of how to prevent the AI and its successors from wreaking havoc. Where “wreaking havoc” could mean anything from turbocharging propaganda and academic cheating, to dispensing bioterrorism advice, to, yes, destroying the world.

You know how you, 11-year-old Scott, set out to write a QBasic program to converse with the user while following Asimov’s Three Laws of Robotics? You know how you quickly got stuck?  Thirty years later, imagine everything’s come full circle.  You’re back to the same problem. You’re still stuck.

Oh all right. Maybe I’m just pulling your leg again … like with the Trump thing. Maybe you can tell because of all the recycled science fiction tropes in this story. Reality would have more imagination than this, wouldn’t it?

But supposing not, what would you want me to do in such a situation?  Don’t worry, I’m not going to take an 11-year-old’s advice without thinking it over first, without bringing to bear whatever I know that you don’t.  But you can look at the situation with fresh eyes, without the 30 intervening years that render it familiar. Help me. Throw me a frickin’ bone here (don’t worry, in five more years you’ll understand the reference).

Thanks!!
—Scott

PS. When something called “bitcoin” comes along, invest your life savings in it, hold for a decade, and then sell.

PPS. About the bullies, and girls, and dating … I could tell you things that would help you figure it out a full decade earlier. If I did, though, you’d almost certainly marry someone else and have a different family. And, see, I’m sort of committed to the family that I have now. And yeah, I know, the mere act of my sending this letter will presumably cause a butterfly effect and change everything anyway, yada yada.  Even so, I feel like I owe it to my current kids to maximize their probability of being born.  Sorry, bud!

Update (Dec. 6): I’m having a blast at the Workshop on Spacetime and Quantum Information at the Institute for Advanced Study in Princeton. I’m learning a huge amount from the talks and discussions here—and also simply enjoying being back in Princeton, to see old friends and visit old haunts like the Bent Spoon. Tomorrow I’ll speak about my recent work with Jason Pollack on polynomial-time AdS bulk reconstruction. [New: click here for video of my talk!]

But there’s one thing, relevant to this post, that I can’t let pass without comment. Tonight, David Nirenberg, Director of the IAS and a medieval historian, gave an after-dinner speech to our workshop, centered around how auspicious it was that the workshop was being held a mere week after the momentous announcement of a holographic wormhole on a microchip (!!)—a feat that experts were calling the first-ever laboratory investigation of quantum gravity, and a new frontier for experimental physics itself. Nirenberg asked whether, a century from now, people might look back on the wormhole achievement as today we look back on Eddington’s 1919 eclipse observations providing the evidence for general relativity.

I confess: this was the first time I felt visceral anger, rather than mere bemusement, over this wormhole affair. Before, I had implicitly assumed: no one was actually hoodwinked by this. No one really, literally believed that this little 9-qubit simulation opened up a wormhole, or helped prove the holographic nature of the real universe, or anything like that. I was wrong.

To be clear, I don’t blame Professor Nirenberg at all. If I were a medieval historian, everything he said about the experiment’s historic significance might strike me as perfectly valid inferences from what I’d read in the press. I don’t blame the It from Qubit community—most of which, I can report, was grinding its teeth and turning red in the face right alongside me. I don’t even blame most of the authors of the wormhole paper, such as Daniel Jafferis, who gave a perfectly sober, reasonable, technical talk at the workshop about how he and others managed to compress a simulation of a variant of the SYK model into a mere 9 qubits—a talk that eschewed all claims of historic significance and of literal wormhole creation.

But it’s now clear to me that, between

(1) the It from Qubit community that likes to explore speculative ideas like holographic wormholes, and

(2) the lay news readers who are now under the impression that Google just did one of the greatest physics experiments of all time,

something went terribly wrong—something that risks damaging trust in the scientific process itself. And I think it’s worth reflecting on what we can do to prevent it from happening again.

---

This is going to be one of the many Shtetl-Optimized posts that I didn’t feel like writing, but was given no choice but to write.

News, social media, and my inbox have been abuzz with two claims about Google’s Sycamore quantum processor, the one that now has 72 superconducting qubits.

The first claim is that Sycamore created a wormhole (!)—a historic feat possible only with a quantum computer. See for example the New York Times and Quanta and Ars Technica and Nature (and of course, the actual paper), as well as Peter Woit’s blog and Chad Orzel’s blog.

The second claim is that Sycamore’s pretensions to quantum supremacy have been refuted. The latter claim is based on this recent preprint by Dorit Aharonov, Xun Gao, Zeph Landau, Yunchao Liu, and Umesh Vazirani. No one—least of all me!—doubts that these authors have proved a strong new technical result, solving a significant open problem in the theory of noisy random circuit sampling. On the other hand, it might be less obvious how to interpret their result and put it in context. See also a YouTube video of Yunchao speaking about the new result at this week’s Simons Institute Quantum Colloquium, and of a panel discussion afterwards, where Yunchao, Umesh Vazirani, Adam Bouland, Sergio Boixo, and your humble blogger discuss what it means.

On their face, the two claims about Sycamore might seem to be in tension. After all, if Sycamore can’t do anything beyond what a classical computer can do, then how exactly did it bend the topology of spacetime?

I submit that neither claim is true. On the one hand, Sycamore did not “create a wormhole.” On the other hand, it remains pretty hard to simulate with a classical computer, as far as anyone knows. To summarize, then, our knowledge of what Sycamore can and can’t do remains much the same as last week or last month!

---

Let’s start with the wormhole thing. I can’t really improve over how I put it in Dennis Overbye’s NYT piece:

“The most important thing I’d want New York Times readers to understand is this,” Scott Aaronson, a quantum computing expert at the University of Texas in Austin, wrote in an email. “If this experiment has brought a wormhole into actual physical existence, then a strong case could be made that you, too, bring a wormhole into actual physical existence every time you sketch one with pen and paper.”

More broadly, Overbye’s NYT piece explains with admirable clarity what this experiment did and didn’t do—leaving only the question “wait … if that’s all that’s going on here, then why is it being written up in the NYT??” This is a rare case where, in my opinion, the NYT did a much better job than Quanta, which unequivocally accepted and amplified the “QC creates a wormhole” framing.

Alright, but what’s the actual basis for the “QC creates a wormhole” claim, for those who don’t want to leave this blog to read about it? Well, the authors used 9 of Sycamore’s 72 qubits to do a crude simulation of something called the SYK (Sachdev-Ye-Kitaev) model. SYK has become popular as a toy model for quantum gravity. In particular, it has a holographic dual description, which can indeed involve a spacetime with one or more wormholes. So, they ran a quantum circuit that crudely modelled the SYK dual of a scenario with information sent through a wormhole. They then confirmed that the circuit did what it was supposed to do—i.e., what they’d already classically calculated that it would do.

So, the objection is obvious: if someone simulates a black hole on their classical computer, they don’t say they thereby “created a black hole.” Or if they do, journalists don’t uncritically repeat the claim. Why should the standards be different just because we’re talking about a quantum computer rather than a classical one?

Did we at least learn anything new about SYK wormholes from the simulation? Alas, not really, because 9 qubits take a mere 2⁹=512 complex numbers to specify their wavefunction, and are therefore trivial to simulate on a laptop. There’s some argument in the paper that, if the simulation were scaled up to (say) 100 qubits, then maybe we would learn something new about SYK. Even then, however, we’d mostly learn about certain corrections that arise because the simulation was being done with “only” n=100 qubits, rather than in the n→∞ limit where SYK is rigorously understood. But while those corrections, arising when n is “neither too large nor too small,” would surely be interesting to specialists, they’d have no obvious bearing on the prospects for creating real physical wormholes in our universe.

And yet, this is not a sensationalistic misunderstanding invented by journalists. Some prominent quantum gravity theorists themselves—including some of my close friends and collaborators—persist in talking about the simulated SYK wormhole as “actually being” a wormhole. What are they thinking?

Daniel Harlow explained the thinking to me as follows (he stresses that he’s explaining it, not necessarily endorsing it). If you had two entangled quantum computers, one on Earth and the other in the Andromeda galaxy, and if they were both simulating SYK, and if Alice on Earth and Bob in Andromeda both uploaded their own brains into their respective quantum simulations, then it seems possible that the simulated Alice and Bob could have the experience of jumping into a wormhole and meeting each other in the middle. Granted, they couldn’t get a message back out from the wormhole, at least not without “going the long way,” which could happen only at the speed of light—so only simulated-Alice and simulated-Bob themselves could ever test this prediction. Nevertheless, if true, I suppose some would treat it as grounds for regarding a quantum simulation of SYK as “more real” or “more wormholey” than a classical simulation.

Of course, this scenario depends on strong assumptions not merely about quantum gravity, but also about the metaphysics of consciousness! And I’d still prefer to call it a simulated wormhole for simulated people.

For completeness, here’s Harlow’s passage from the NYT article:

Daniel Harlow, a physicist at M.I.T. who was not involved in the experiment, noted that the experiment was based on a model of quantum gravity that was so simple, and unrealistic, that it could just as well have been studied using a pencil and paper.

“So I’d say that this doesn’t teach us anything about quantum gravity that we didn’t already know,” Dr. Harlow wrote in an email. “On the other hand, I think it is exciting as a technical achievement, because if we can’t even do this (and until now we couldn’t), then simulating more interesting quantum gravity theories would CERTAINLY be off the table.” Developing computers big enough to do so might take 10 or 15 years, he added.

---

Alright, let’s move on to the claim that quantum supremacy has been refuted. What Aharonov et al. actually show in their new work, building on earlier work by Gao and Duan, is that Random Circuit Sampling, with a constant rate of noise per gate and no error-correction, can’t provide a scalable approach to quantum supremacy. Or more precisely: as the number of qubits n goes to infinity, and assuming you’re in the “anti-concentration regime” (which in practice probably means: the depth of your quantum circuit is at least ~log(n)), there’s a classical algorithm to approximately sample the quantum circuit’s output distribution in poly(n) time (albeit, not yet a practical algorithm).

Here’s what’s crucial to understand: this is 100% consistent with what those of us working on quantum supremacy had assumed since at least 2016! We knew that if you tried to scale Random Circuit Sampling to 200 or 500 or 1000 qubits, while you also increased the circuit depth proportionately, the signal-to-noise ratio would become exponentially small, meaning that your quantum speedup would disappear. That’s why, from the very beginning, we targeted the “practical” regime of 50-100 qubits: a regime where

1. you can still see explicitly that you’re exploiting a 2⁵⁰– or 2¹⁰⁰-dimensional Hilbert space for computational advantage, thereby confirming one of the main predictions of quantum computing theory, but
2. you also have a signal that (as it turned out) is large enough to see with heroic effort.

To their credit, Aharonov et al. explain all this perfectly clearly in their abstract and introduction. I’m just worried that others aren’t reading their paper as carefully as they should be!

So then, what’s the new advance in the Aharonov et al. paper? Well, there had been some hope that circuit depth ~log(n) might be a sweet spot, where an exponential quantum speedup might both exist and survive constant noise, even in the asymptotic limit of n→∞ qubits. Nothing in Google’s or USTC’s actual Random Circuit Sampling experiments depended on that hope, but it would’ve been nice if it were true. What Aharonov et al. have now done is to kill that hope, using powerful techniques involving summing over Feynman paths in the Pauli basis.

Stepping back, what is the current status of quantum supremacy based on Random Circuit Sampling? I would say it’s still standing, but more precariously than I’d like—underscoring the need for new and better quantum supremacy experiments. In more detail, Pan, Chen, and Zhang have shown how to simulate Google’s 53-qubit Sycamore chip classically, using what I estimated to be 100-1000X the electricity cost of running the quantum computer itself (including the dilution refrigerator!). Approaching from the problem from a different angle, Gao et al. have given a polynomial-time classical algorithm for spoofing Google’s Linear Cross-Entropy Benchmark (LXEB)—but their algorithm can currently achieve only about 10% of the excess in LXEB that Google’s experiment found.

So, though it’s been under sustained attack from multiple directions these past few years, I’d say that the flag of quantum supremacy yet waves. The Extended Church-Turing Thesis is still on thin ice. The wormhole is still open. Wait … no … that’s not what I meant to write…

---

Note: With this post, as with future science posts, all off-topic comments will be ruthlessly left in moderation. Yes, even if the comments “create their own reality” full of anger and disappointment that I talked about what I talked about, instead of what the commenter wanted me to talk about. Even if merely refuting the comments would require me to give in and talk about their preferred topics after all. Please stop. This is a wormholes-‘n-supremacy post.

Update (Nov. 22): Theoretical computer scientist and longtime friend-of-the-blog Boaz Barak writes to tell me that, coincidentally, he and Ben Edelman just released a big essay advocating a version of “Reform AI Alignment” on Boaz’s Windows on Theory blog, as well as on LessWrong. (I warned Boaz that, having taken the momentous step of posting to LessWrong, in 6 months he should expect to find himself living in a rationalist group house in Oakland…) Needless to say, I don’t necessarily endorse their every word or vice versa, but there’s a striking amount of convergence. They also have a much more detailed discussion of (e.g.) which kinds of optimization processes they consider relatively safe.

---

Nearly halfway into my year at OpenAI, still reeling from the FTX collapse, I feel like it’s finally time to start blogging my AI safety thoughts—starting with a little appetizer course today, more substantial fare to come.

Many people claim that AI alignment is little more a modern eschatological religion—with prophets, an end-times prophecy, sacred scriptures, and even a god (albeit, one who doesn’t exist quite yet). The obvious response to that claim is that, while there’s some truth to it, “religions” based around technology are a little different from the old kind, because technological progress actually happens regardless of whether you believe in it.

I mean, the Internet is sort of like the old concept of the collective unconscious, except that it actually exists and you’re using it right now. Airplanes and spacecraft are kind of like the ancient dream of Icarus—except, again, for the actually existing part. Today GPT-3 and DALL-E2 and LaMDA and AlphaTensor exist, as they didn’t two years ago, and one has to try to project forward to what their vastly-larger successors will be doing a decade from now. Though some of my colleagues are still in denial about it, I regard the fact that such systems will have transformative effects on civilization, comparable to or greater than those of the Internet itself, as “already baked in”—as just the mainstream position, not even a question anymore. That doesn’t mean that future AIs are going to convert the earth into paperclips, or give us eternal life in a simulated utopia. But their story will be a central part of the story of this century.

Which brings me to a second response. If AI alignment is a religion, it’s now large and established enough to have a thriving “Reform” branch, in addition to the original “Orthodox” branch epitomized by Eliezer Yudkowsky and MIRI.  As far as I can tell, this Reform branch now counts among its members a large fraction of the AI safety researchers now working in academia and industry.  (I’ll leave the formation of a Conservative branch of AI alignment, which reacts against the Reform branch by moving slightly back in the direction of the Orthodox branch, as a problem for the future — to say nothing of Reconstructionist or Marxist branches.)

Here’s an incomplete but hopefully representative list of the differences in doctrine between Orthodox and Reform AI Risk:

(1) Orthodox AI-riskers tend to believe that humanity will survive or be destroyed based on the actions of a few elite engineers over the next decade or two.  Everything else—climate change, droughts, the future of US democracy, war over Ukraine and maybe Taiwan—fades into insignificance except insofar as it affects those engineers.

We Reform AI-riskers, by contrast, believe that AI might well pose civilizational risks in the coming century, but so does all the other stuff, and it’s all tied together.  An invasion of Taiwan might change which world power gets access to TSMC GPUs.  Almost everything affects which entities pursue the AI scaling frontier and whether they’re cooperating or competing to be first.

(2) Orthodox AI-riskers believe that public outreach has limited value: most people can’t understand this issue anyway, and will need to be saved from AI despite themselves.

We Reform AI-riskers believe that trying to get a broad swath of the public on board with one’s preferred AI policy is something close to a deontological imperative.

(3) Orthodox AI-riskers worry almost entirely about an agentic, misaligned AI that deceives humans while it works to destroy them, along the way to maximizing its strange utility function.

We Reform AI-riskers entertain that possibility, but we worry at least as much about powerful AIs that are weaponized by bad humans, which we expect to pose existential risks much earlier in any case.

(4) Orthodox AI-riskers have limited interest in AI safety research applicable to actually-existing systems (LaMDA, GPT-3, DALL-E2, etc.), seeing the dangers posed by those systems as basically trivial compared to the looming danger of a misaligned agentic AI.

We Reform AI-riskers see research on actually-existing systems as one of the only ways to get feedback from the world about which AI safety ideas are or aren’t promising.

(5) Orthodox AI-riskers worry most about the “FOOM” scenario, where some AI might cross a threshold from innocuous-looking to plotting to kill all humans in the space of hours or days.

We Reform AI-riskers worry most about the “slow-moving trainwreck” scenario, where (just like with climate change) well-informed people can see the writing on the wall decades ahead, but just can’t line up everyone’s incentives to prevent it.

(6) Orthodox AI-riskers talk a lot about a “pivotal act” to prevent a misaligned AI from ever being developed, which might involve (e.g.) using an aligned AI to impose a worldwide surveillance regime.

We Reform AI-riskers worry more about such an act causing the very calamity that it was intended to prevent.

(7) Orthodox AI-riskers feel a strong need to repudiate the norms of mainstream science, seeing them as too slow-moving to react in time to the existential danger of AI.

We Reform AI-riskers feel a strong need to get mainstream science on board with the AI safety program.

(8) Orthodox AI-riskers are maximalists about the power of pure, unaided superintelligence to just figure out how to commandeer whatever physical resources it needs to take over the world (for example, by messaging some lab over the Internet, and tricking it into manufacturing nanobots that will do the superintelligence’s bidding).

We Reform AI-riskers believe that, here just like in high school, there are limits to the power of pure intelligence to achieve one’s goals.  We’d expect even an agentic, misaligned AI, if such existed, to need a stable power source, robust interfaces to the physical world, and probably allied humans before it posed much of an existential threat.

What have I missed?

Update (Dec. 15): This, by former Shtetl-Optimized guest blogger Sarah Constantin, is the post about SBF that I should’ve written and wish I had written.

Update (Nov. 16): Check out this new interview of SBF by my friend and leading Effective Altruist writer Kelsey Piper. Here Kelsey directly confronts SBF with some of the same moral and psychological questions that animated this post and the ensuing discussion—and, surely to the consternation of his lawyers, SBF answers everything she asks. And yet I still don’t know what exactly to make of it. SBF’s responses reveal a surprising cynicism (surprising because, if you’re that cynical, why be open about it?), as well as an optimism that he can still fix everything that seems wildly divorced from reality.

I still stand by most of the main points of my post, including:

• the technical insanity of SBF’s clearly-expressed attitude to risk (“gambler’s ruin? more like gambler’s opportunity!!”), and its probable role in creating the conditions for everything that followed,
• the need to diagnose the catastrophe correctly (making billions of dollars in order to donate them to charity? STILL VERY GOOD; lying and raiding customer deposits in course of doing so? DEFINITELY BAD), and
• how, when sneerers judge SBF guilty just for being a crypto billionaire who talked about Effective Altruism, it ironically lets him off the hook for what he specifically did that was terrible.

But over the past couple days, I’ve updated in the direction of understanding SBF’s psychology a lot less than I thought I did. While I correctly hit on certain aspects of the tragedy, there are other important aspects—the drug use, the cynical detachment (“life as a video game”), the impulsivity, the apparent lying—that I neglected to touch on and about which we’ll surely learn more in the coming days, weeks, and years. –SA

---

Several readers have asked me for updated thoughts on AI safety, now that I’m 5 months into my year at OpenAI—and I promise, I’ll share them soon! The thing is, until last week I’d entertained the idea of writing up some of those thoughts for an essay competition run by the FTX Future Fund, which (I was vaguely aware) was founded by the cryptocurrency billionaire Sam Bankman-Fried, henceforth SBF.

Alas, unless you’ve been tucked away on some Caribbean island—or perhaps, especially if you have been—you’ll know that the FTX Future Fund has ceased to exist. In the course of 2-3 days last week, SBF’s estimated net worth went from ~$15 billion to a negative number, possibly the fastest evaporation of such a vast personal fortune in all human history. Notably, SBF had promised to give virtually all of it away to various worthy causes, including mitigating existential risk and helping Democrats win elections, and the worldwide Effective Altruist community had largely reoriented itself around that pledge. That’s all now up in smoke.

I’ve never met SBF, although he was a physics undergraduate at MIT while I taught CS there. What little I knew of SBF before this week, came mostly from reading Gideon Lewis-Kraus’s excellent New Yorker article about Effective Altruism this summer. The details of what happened at FTX are at once hopelessly complicated and—it would appear—damningly simple, involving the misuse of billions of dollars’ worth of customer deposits to place risky bets that failed. SBF has, in any case, tweeted that he “fucked up and should have done better.”

You’d think none of this would directly impact me, since SBF and I inhabit such different worlds. He ran a crypto empire from the Bahamas, sharing a group house with other twentysomething executives who often dated each other. I teach at a large state university and try to raise two kids. He made his first fortune by arbitraging bitcoin between Asia and the West. I own, I think, a couple bitcoins that someone gave me in 2016, but have no idea how to access them anymore. His hair is large and curly; mine is neither.

Even so, I’ve found myself obsessively following this story because I know that, in a broader sense, I will be called to account for it. SBF and I both grew up as nerdy kids in middle-class Jewish American families, and both had transformative experiences as teenagers at Canada/USA Mathcamp. He and I know many of the same people. We’ve both been attracted to the idea of small groups of idealistic STEM nerds using their skills to help save the world from climate change, pandemics, and fascism.

Aha, the sneerers will sneer! Hasn’t the entire concept of “STEM nerds saving the world” now been utterly discredited, revealed to be just a front for cynical grifters and Ponzi schemers? So if I’m also a STEM nerd who’s also dreamed of helping to save the world, then don’t I stand condemned too?

I’m writing this post because, if the Greek tragedy of SBF is going to be invoked as a cautionary tale in nerd circles forevermore—which it will be—then I think it’s crucial that we tell the right cautionary tale.

It’s like, imagine the Apollo 11 moon mission had almost succeeded, but because of a tiny crack in an oxygen tank, it instead exploded in lunar orbit, killing all three of the astronauts. Imagine that the crack formed partly because, in order to hide a budget overrun, Wernher von Braun had secretly substituted a cheaper material, while telling almost none of his underlings.

There are many excellent lessons that one could draw from such a tragedy, having to do with, for example, the construction of oxygen tanks, the procedures for inspecting them, Wernher von Braun as an individual, or NASA safety culture.

But there would also be bad lessons to not draw. These include: “The entire enterprise of sending humans to the moon was obviously doomed from the start.” “Fate will always punish human hubris.” “All the engineers’ supposed quantitative expertise proved to be worthless.”

From everything I’ve read, SBF’s mission to earn billions, then spend it saving the world, seems something like this imagined Apollo mission. Yes, the failure was total and catastrophic, and claimed innocent victims. Yes, while bad luck played a role, so did, shall we say, fateful decisions with a moral dimension. If it’s true that, as alleged, FTX raided its customers’ deposits to prop up the risky bets of its sister organization Alameda Research, multiple countries’ legal systems will surely be sorting out the consequences for years.

To my mind, though, it’s important not to minimize the gravity of the fateful decision by conflating it with everything that preceded it. I confess to taking this sort of conflation extremely personally. For eight years now, the rap against me, advanced by thousands (!) on social media, has been: sure, while by all accounts Aaronson is kind and respectful to women, he seems like exactly the sort of nerdy guy who, still bitter and frustrated over high school, could’ve chosen instead to sexually harass women and hinder their scientific careers. In other words, I stand condemned by part of the world, not for the choices I made, but for choices I didn’t make that are considered “too close to me” in the geometry of conscience.

And I don’t consent to that. I don’t wish to be held accountable for the misdeeds of my doppelgängers in parallel universes. Therefore, I resolve not to judge anyone else by their parallel-universe doppelgängers either. If SBF indeed gambled away his customers’ deposits and lied about it, then I condemn him for it utterly, but I refuse to condemn his hypothetical doppelgänger who didn’t do those things.

Granted, there are those who think all cryptocurrency is a Ponzi scheme and a scam, and that for that reason alone, it should’ve been obvious from the start that crypto-related plans could only end in catastrophe. The “Ponzi scheme” theory of cryptocurrency has, we ought to concede, a substantial case in its favor—though I’d rather opine about the matter in (say) 2030 than now. Like many technologies that spend years as quasi-scams until they aren’t, maybe blockchains will find some compelling everyday use-cases, besides the well-known ones like drug-dealing, ransomware, and financing rogue states.

Even if cryptocurrency remains just a modern-day tulip bulb or Beanie Baby, though, it seems morally hard to distinguish a cryptocurrency trader from the millions who deal in options, bonds, and all manner of other speculative assets. And a traditional investor who made billions on successful gambles, or arbitrage, or creating liquidity, then gave virtually all of it away to effective charities, would seem, on net, way ahead of most of us morally.

To be sure, I never pursued the “Earning to Give” path myself, though certainly the concept occurred to me as a teenager, before it had a name. Partly I decided against it because I seem to lack a certain brazenness, or maybe just willingness to follow up on tedious details, needed to win in business. Partly, though, I decided against trying to get rich because I’m selfish (!). I prioritized doing fascinating quantum computing research, starting a family, teaching, blogging, and other stuff I liked over devoting every waking hour to possibly earning a fortune only to give it all to charity, and more likely being a failure even at that. All told, I don’t regret my scholarly path—especially not now!—but I’m also not going to encase it in some halo of obvious moral superiority.

If I could go back in time and give SBF advice—or if, let’s say, he’d come to me at MIT for advice back in 2013—what could I have told him? I surely wouldn’t talk about cryptocurrency, about which I knew and know little. I might try to carve out some space for deontological ethics against pure utilitarianism, but I might also consider that a lost cause with this particular undergrad.

On reflection, maybe I’d just try to convince SBF to weight money logarithmically when calculating expected utility (as in the Kelly criterion), to forsake the linear weighting that SBF explicitly advocated and that he seems to have put into practice in his crypto ventures. Or if not logarithmic weighing, I’d try to sell him on some concave utility function—something that makes, let’s say, a mere $1 billion in hand seem better than $15 billion that has a 50% probability of vanishing and leaving you, your customers, your employees, and the entire Effective Altruism community with less than nothing.

At any rate, I’d try to impress on him, as I do on anyone reading now, that the choice between linear and concave utilities, between risk-neutrality and risk-aversion, is not bloodless or technical—that it’s essential to make a choice that’s not only in reflective equilibrium with your highest values, but that you’ll still consider to be such regardless of which possible universe you end up in.